
【题目】已知曲线C1的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ. (Ⅰ)把C1的参数方程化为极坐标方程;
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ. (Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
【答案】解:(Ⅰ)曲线C1的参数方程为 ![]() (t为参数), 则曲线C1的普通方程为(x﹣5)2+(y﹣4)2=25,
(t为参数), 则曲线C1的普通方程为(x﹣5)2+(y﹣4)2=25,
曲线C1的极坐标方程为ρ2﹣10ρcosθ﹣8ρsinθ+16=0.
(Ⅱ)曲线C1的极坐标方程ρ2﹣10ρcosθ﹣8ρsinθ+16=0,曲线C2的极坐标方程为ρ=2cosθ,联立得 ![]() ,又θ∈[0,2π),则θ=0或
,又θ∈[0,2π),则θ=0或 ![]() ,
,
当θ=0时,ρ=2;当 ![]() 时,
时, ![]() ,所以交点坐标为(2,0),
,所以交点坐标为(2,0), ![]()
【解析】(Ⅰ)把C1的参数方程化为普通方程,再化为极坐标方程;(Ⅱ)曲线C1的极坐标方程ρ2﹣10ρcosθ﹣8ρsinθ+16=0,曲线C2的极坐标方程为ρ=2cosθ,联立,即可求C1与C2交点的极坐标.


科目:高中数学 来源: 题型:
【题目】已知椭圆C以原点为中心,左焦点F的坐标是(﹣1,0),长轴长是短轴长的 ![]() 倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;
倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°; 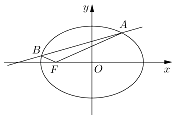
(1)求椭圆C的标准方程;
(2)对于动直线l,是否存在一个定点,无论∠OFA如何变化,直线l总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△AnBnCn的三边长分别为an , bn , cn , △AnBnCn的面积为Sn , n=1,2,3…若b1>c1 , b1+c1=2a1 , an+1=an , ![]() ,
, ![]() ,则( )
,则( )
A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n﹣1}为递增数列,{S2n}为递减数列
D.{S2n﹣1}为递减数列,{S2n}为递增数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},a1=a(a∈R),an+1= ![]() (n∈N*).
(n∈N*).
(1)若数列{an}从第二项起每一项都大于1,求实数a的取值范围;
(2)若a=﹣3,记Sn是数列{an}的前n项和,证明:Sn<n+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1+2a2+…+nan=4﹣ ![]() .
.
(1)求数列{an}的通项公式;
(2)若bn=(3n﹣2)an , 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos( ![]() ﹣x)cos(x+
﹣x)cos(x+ ![]() )+
)+ ![]() . (Ⅰ)求函数f(x)的最小正周期和单调递减区间;
. (Ⅰ)求函数f(x)的最小正周期和单调递减区间;
(Ⅱ)求函数f(x)在区间[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,D在AB上,AD:DB=1:2,E为AC中点,CD、BE相交于点P,连结AP.设 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),则x,y的值分别为( )
(x,y∈R),则x,y的值分别为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣axlnx(a∈R)在x=1处的切线方程为y=bx+1+
﹣axlnx(a∈R)在x=1处的切线方程为y=bx+1+ ![]() (b∈R).
(b∈R).
(1)求a,b的值;
(2)证明:f(x)< ![]() .
.
(3)若正实数m,n满足mn=1,证明: ![]() +
+ ![]() <2(m+n).
<2(m+n).
查看答案和解析>>
科目:高中数学 来源: 题型:
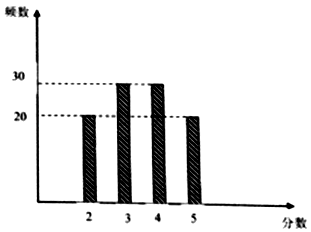
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
等级 | 不好 | 较好 | 优良 |
奖惩标准(元) | ﹣1000 | 2000 | 3000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com