
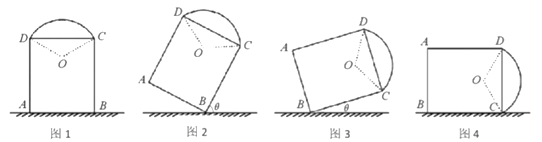
【题目】如图1,一艺术拱门由两部分组成,下部为矩形![]() 的长分别为
的长分别为![]() 米和
米和![]() 米,上部是圆心为
米,上部是圆心为![]() 的劣弧
的劣弧![]() ,
,![]()
(1)求图1中拱门最高点到地面的距离:
(2)现欲以![]() 点为支点将拱门放倒,放倒过程中矩形
点为支点将拱门放倒,放倒过程中矩形![]() 所在的平面始终与地面垂直,如图2、图3、图4所示,设
所在的平面始终与地面垂直,如图2、图3、图4所示,设![]() 与地面水平线
与地面水平线![]() 所成的角为
所成的角为![]() .若拱门上的点到地面的最大距离恰好为
.若拱门上的点到地面的最大距离恰好为![]() 到地面的距离,试求
到地面的距离,试求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() 及
及![]() ,可求得圆的半径,根据最高点与圆心的关系即可求得到地面的距离.
,可求得圆的半径,根据最高点与圆心的关系即可求得到地面的距离.
(2)通过讨论P点所在的位置以及三角函数的性质可判断出h取最大值时θ取值范围.
(1)过O点作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() .如下图所示:
.如下图所示:
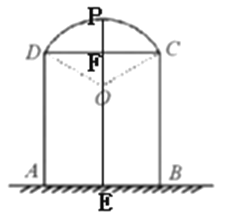
则![]() 即为所求.
即为所求.
因为![]() ,
,![]()
所以
则![]()
所以![]()
即拱门最高点到地面的距离为5米
(2)在拱门放倒过程中,过点O作与地面垂直的直线与“拱门外框上沿”相交于点P.
当点P在劣弧CD上时,拱门上的点到地面的最大距离h等于圆O的半径长与圆心O到地面距离之和;
当点P在线段AD上时,拱门上的点到地面的最大距离h等于点D到地面的距离.
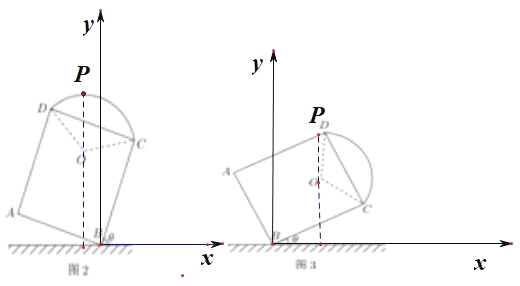
由(1)知,在Rt△OO1B中,OB![]() 2
2![]() .
.
以B为坐标原点,直线l为x轴,建立如图所示的坐标系.
①当点P在劣弧CD上时,![]() .
.
由∠OBx=θ![]() ,OB=2
,OB=2 ![]() ,
,
由三角函数定义,得O(2![]() cos(
cos(![]() ),2
),2![]() ),
),
则h=2+2![]() ,所以当θ
,所以当θ![]() 即θ
即θ![]() 时,h取得最大值2+2
时,h取得最大值2+2![]() ,
,
②当点P在线段AD上时,0≤θ![]() .
.
设∠CBD=φ,在Rt△BCD中,DB![]() 2
2![]() ,sinφ
,sinφ![]() ,cosφ
,cosφ![]() .
.
由∠DBx=θ+φ,得D(2![]() (θ+φ),2
(θ+φ),2![]() (θ+φ)).
(θ+φ)).
所以h=2![]() (θ+φ)=4sinθ+2
(θ+φ)=4sinθ+2![]() cosθ,
cosθ,
又当0<θ![]() 时,h′=4cosθ﹣2
时,h′=4cosθ﹣2![]() sinθ>4cos
sinθ>4cos![]() 2
2![]() sin
sin ![]() 0,
0,
所以h=4sinθ+2![]() 在[0,
在[0,![]() ]上递增.
]上递增.
所以当θ![]() 时,h取得最大值5.
时,h取得最大值5.
因为2+2![]() 5,所以h的最大值为2+2
5,所以h的最大值为2+2![]() .
.
综上,若拱门上的点到地面的最大距离恰好为D到地面的距离,则θ![]() .
.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】若![]() 是递增数列,数列
是递增数列,数列![]() 满足:对任意
满足:对任意![]() ,存在
,存在![]() ,使得
,使得![]() ,则称
,则称![]() 是
是![]() 的“分隔数列”.
的“分隔数列”.
(1)设![]() ,证明:数列
,证明:数列![]() 是
是![]() 的分隔数列;
的分隔数列;
(2)设![]() 是
是![]() 的前n项和,
的前n项和,![]() ,判断数列
,判断数列![]() 是否是数列
是否是数列![]() 的分隔数列,并说明理由;
的分隔数列,并说明理由;
(3)设![]() 是
是![]() 的前n项和,若数列
的前n项和,若数列![]() 是
是![]() 的分隔数列,求实数
的分隔数列,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
(1)求抛物线G的方程;
(2)如图,过抛物线G的焦点的直线依次与抛物线G及圆x2+(y﹣1)2=1交于A、C、D、B四点,试证明|AC||BD|为定值;
(3)过A、B分别作抛物G的切线l1,l2且l1,l2交于点M,试求△ACM与△BDM面积之和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数据![]() ,
,![]() ,
,![]() ,
,![]() 是上海普通职
是上海普通职![]() (
(![]() ,
,![]() )个人的年收入,设这
)个人的年收入,设这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确( )
个数据中,下列说法正确( )
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数大大增大,中位数可能不变,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,如果存在两条平行直线
,如果存在两条平行直线![]() 与
与![]()
![]() ,使得对于任意
,使得对于任意![]() ,都有
,都有![]() 恒成立,那么称函数
恒成立,那么称函数![]() 是带状函数,若
是带状函数,若![]() ,
,![]() 之间的最小距离
之间的最小距离![]() 存在,则称
存在,则称![]() 为带宽.
为带宽.
(1)判断函数![]() 是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
(2)求证:函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)求证:函数![]() (
(![]() )为带状函数的充要条件是
)为带状函数的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张,为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少0.5万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数量构成数列![]() ,每年发放电动型汽车牌照数为构成数列
,每年发放电动型汽车牌照数为构成数列![]() ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 过点
过点![]() ,且渐近线方程为
,且渐近线方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于点
交于点![]() 、
、![]() 两点.
两点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 过原点,点
过原点,点![]() 是曲线
是曲线![]() 上任一点,直线
上任一点,直线![]() ,
,![]() 的斜率都存在,记为
的斜率都存在,记为![]() 、
、![]() ,试探究
,试探究![]() 的值是否与点
的值是否与点![]() 及直线
及直线![]() 有关,并证明你的结论;
有关,并证明你的结论;
(3)若直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 坐标及此常数的值;若不存在,说明理由.
坐标及此常数的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为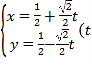 为参数), 椭圆C的参数方程为
为参数), 椭圆C的参数方程为![]() 为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2,
为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2, ![]()
(1)求椭圆C的直角坐标方程和点A在直角坐标系下的坐标
(2)直线l与椭圆C交于P,Q两点,求△APQ的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com