
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� �٣�����0���ķ��ǡ���0����
�ڣ�����ķ����������ͽ���ͬʱ��
�ۣ�������p��qΪ�桱��������p��q��һ��Ϊ�桱��
�ܣ�a1=2��a1��a3��a4�ɵȱ����У���dΪ$-\frac{1}{2}$��0��
��� �⣺���ڢ٣����⡰?x��R��x2-x��0���ķ��ǡ�?x��R��x2-x��0�����ʴ���
���ڢڣ����⡰��a��b����2a��2b-1���ķ�����Ϊ����a��b����2a��2b-1������ȷ��
���ڢۣ�������p��qΪ�桱�ǡ�����p��qΪ�桱�ı�Ҫ������������ʴ���
���ڢܣ��ڹ���Ϊd�ĵȲ�����{an}�У�a1=2��a1��a3��a4�ɵȱ����У���dΪ$-\frac{1}{2}$��0���ʴ���
��ѡ��B
���� ���⿼�������������ж������ڻ����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
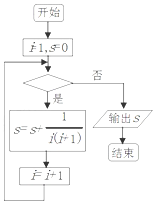 һ���㷨�Ŀ�ͼ����ͼ��ʾ�����ó�������Ľ��Ϊ$\frac{5}{6}$�����жϿ���Ӧ����������ǣ�������
һ���㷨�Ŀ�ͼ����ͼ��ʾ�����ó�������Ľ��Ϊ$\frac{5}{6}$�����жϿ���Ӧ����������ǣ�������| A�� | i��6 | B�� | i��6 | C�� | i��5 | D�� | i��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $f��{\frac{{{x_1}+{x_2}}}{2}}����\frac{{f��{x_1}��+f��{x_2}��}}{2}$ | B�� | $f��{\frac{{{x_1}+{x_2}}}{2}}����\frac{{f��{x_1}��+f��{x_2}��}}{2}$ | ||
| C�� | $f��{\frac{{{x_1}+{x_2}}}{2}}��=\frac{{f��{x_1}��+f��{x_2}��}}{2}$ | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\sqrt{2}$ | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��a��b | C�� | a��c��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com