
【题目】设函数f(x)=4x2+ax+2,不等式f(x)<c的解集为(﹣1,2).
(1)求a的值;
(2)解不等式 ![]() .
.
【答案】
(1)解:∵函数f(x)=4x2+ax+2,不等式f(x)<c的解集为(﹣1,2),
∴﹣1+2=﹣ ![]() ,∴a=﹣4
,∴a=﹣4
(2)解:不等式转化为(4x+m)(﹣4x+2)>0,
可得m=﹣2,不等式的解集为;
m<﹣2,不等式的解集为{x| ![]() };
};
m>﹣2,不等式的解集为{x|﹣ ![]() }
}
【解析】(1)利用韦达定理,建立方程,即可求a的值;(2)不等式转化为(4x+m)(﹣4x+2)>0,分类讨论,解不等式.
【考点精析】通过灵活运用解一元二次不等式,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边即可以解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边即可以解答此题.


科目:高中数学 来源: 题型:
【题目】长沙市物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性,对某公司的该产品的销量与价格进行了统计分析,得到如下数据和散点图:
定价 | 10 | 20 | 30 | 40 | 50 | 60 |
年销量 | 1150 | 643 | 424 | 262 | 165 | 86 |
| 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

(参考数据: ![]() ,
,
![]() )
)
(1)根据散点图判断, ![]() 与
与![]() 和
和![]() 与
与![]() 哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字).
的回归方程(方程中的系数均保留两位有效数字).
(3)定价为多少元/ ![]() 时,年销售额的预报值最大?
时,年销售额的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为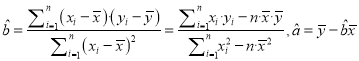 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() :
: ![]() 上,而
上,而![]() 为
为![]() 在
在![]() 轴上的投影,且点
轴上的投影,且点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上两点,且
上两点,且![]() ,
, ![]() 为坐标原点,求
为坐标原点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a1=3,an=2an﹣1+(t+1)2n+3m+t(t,m∈R,n≥2,n∈N*)
(1)t=0,m=0时,求证: ![]() 是等差数列;
是等差数列;
(2)t=﹣1,m= ![]() 是等比数列;
是等比数列;
(3)t=0,m=1时,求数列{an}的通项公式和前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( ) 
A.1000
B.2000
C.3000
D.4000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次测验共有4个选择题和2个填空题,每答对一个选择题得20分,每答对一个填空题得10分,答错或不答得0分,若某同学答对每个选择题的概率均为 ![]() ,答对每个填空题的概率均为
,答对每个填空题的概率均为 ![]() ,且每个题答对与否互不影响.
,且每个题答对与否互不影响.
(1)求该同学得80分的概率;
(2)若该同学已经答对了3个选择题和1个填空题,记他这次测验的得分为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() 为椭圆的半焦距,且
为椭圆的半焦距,且![]() ,过点
,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别交于另两点
分别交于另两点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(3)若线段![]() 的中点在
的中点在![]() 轴上,求直线
轴上,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com