A
分析:根据题意,可得函数y=f'(x)是其定义域上的减函数.由此再结合各图象对应的基本初等函数,利用求导法则求出它们的导数,再讨论导数的单调性,即可得到正确答案.
解答:∵函数g(x)=f(x+t)-f(x)在其定义域内为减函数,
∴g'(x)=f'(x+t)-f'(x)<0在其定义域内恒成立
即f'(x+t)<f'(x),结合t>0,得函数y=f'(x)是其定义域上的减函数.
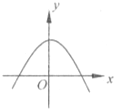
对于A,可设函数f(x)=ax2+bx+c,(a<0)
∴f'(x)=2ax+b,满足在其定义域上为减函数;
对于B,可设f(x)=ax,(0<a<1)
∴f'(x)=axlna,在(0,+∞)上是增函数,不符合题意;
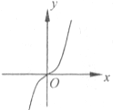
对于C,可设f(x)=x3,可得f'(x)=3x2在其定义域上不是减函数,故C不正确;
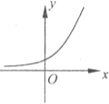
对于D,可设f(x)=ax,(a>1)
∴f'(x)=axlna,在(0,+∞)上是增函数,不符合题意.
故选A
点评:本题给出函数的导数满足的条件,求函数可能的图象.考查了基本初等函数的图象与性质,函数导数与单调性质关系等知识,属于中档题.




 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案