
【题目】如图,在三棱锥P﹣ABC中,AC=![]() BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
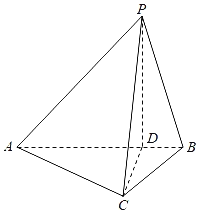
(1)求证:平面PAB⊥平面PCD;
(2)求二面角P﹣AC﹣D的平面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)推导出AC⊥BC,CD⊥AD,PD⊥CD,从而CD⊥平面PAB,由此能证明平面PAB⊥平面PCD.
(2)以D为坐标原点,分别以DC,DB,DP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角P-AC-D的平面角的余弦值.
(1)证明:∵AC=![]() BC,AB=2BC,
BC,AB=2BC,
∴![]() ,
,
∴AB2=AC2+BC2,∴AC⊥BC,
在Rt△ABC中,由AC=![]() BC,得∠CAB=30°,
BC,得∠CAB=30°,
设BD=1,由AD=3BD,得AD=3,BC=2,AC=2![]() ,
,
在△ACD中,由余弦定理得CD2=AD2+AC2﹣2ADACcos30°=3,
∴CD=![]() ,
,
∴CD2+AD2=AC2,∴CD⊥AD,
∵PD⊥平面ABC,CD![]() 平面ABC,
平面ABC,
∴PD⊥CD,
又PD∩AD=D,∴CD⊥平面PAB,
又CD![]() 平面PCD,∴平面PAB⊥平面PCD.
平面PCD,∴平面PAB⊥平面PCD.
(2)解:∵PD⊥平面ABC,
∴PA与平面ABC所成角为∠PAD,即∠PAD=45°,
∴△PAD为等腰直角三角形,PD=AD,
由(1)得PD=AD=3,以D为坐标原点,
分别以DC,DB,DP所在直线为x,y,z轴,建立空间直角坐标系,

则D(0,0,0),C(![]() ,0,0),A(0,﹣3,0),P(0,0,3),
,0,0),A(0,﹣3,0),P(0,0,3),
![]() =(0,﹣3,﹣3),
=(0,﹣3,﹣3),![]() =(
=(![]() ),
),
则![]() =(0,0,3)是平面ACD的一个法向量,
=(0,0,3)是平面ACD的一个法向量,
设平面PAC的一个法向量![]() =(x,y,z),
=(x,y,z),
则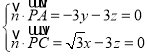 ,取x=
,取x=![]() ,得
,得![]() =(
=(![]() ,﹣1,1),
,﹣1,1),
设二面角P﹣AC﹣D的平面角为θ,
则cosθ=![]() =
=![]() ,
,
∴二面角P﹣AC﹣D的平面角的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)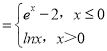 ,g(x)=f(
,g(x)=f(![]() )+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
)+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
A.当k>0时,有2个零点;当k<0时,有4个零点
B.当k>0时,有4个零点;当k<0时,有2个零点
C.无论k为何值,均有2个零点
D.无论k为何值,均有4个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源于中国古代数学家祖冲之的圆周率。公元263年,中国数学家刘徽用“割圆术”计算圆周率,计算到圆内接3072边形的面积,得到的圆周率是![]() .公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率
.公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率![]() 和约率
和约率![]() 。大约在公元530年,印度数学大师阿耶波多算出圆周率约为
。大约在公元530年,印度数学大师阿耶波多算出圆周率约为![]() (
(![]() ).在这4个圆周率的近似值中,最接近真实值的是( )
).在这4个圆周率的近似值中,最接近真实值的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解某产品的销售情况,选择某个电商平台对该产品销售情况作调查.统计了一年内的月销售数量(单位:万件),得到该电商平台月销售数量的茎叶图.
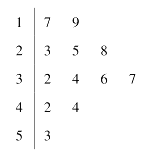
(1)求该电商平台在这一年内月销售该产品数量的中位数和平均数;
(2)该企业与电商签订销售合同时规定:如果电商平台当月的销售件数不低于40万件,当月奖励该电商平台10万元;当月低于40万件没有奖励,用该样本估计总体,从电商平台一个年度内高于该年月销售平均数的月份中任取两个月,求这两个月企业发给电商平台的奖金为20万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央精准扶贫决策,某市将其低收入家庭的基本情况经过统计绘制如图,其中各项统计不重复.若该市老年低收入家庭共有900户,则下列说法错误的是( )
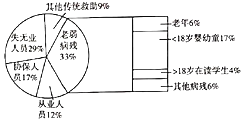
A.该市总有 15000 户低收入家庭
B.在该市从业人员中,低收入家庭共有1800户
C.在该市无业人员中,低收入家庭有4350户
D.在该市大于18岁在读学生中,低收入家庭有 800 户
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设点![]() 分别为曲线
分别为曲线![]() 与曲线
与曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值;
的最大值;
(2)设直线![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com