
【题目】足球运动是一项古老的体育活动,众多的资料表明,中国古代足球的出现比欧洲早,历史更为悠久,如图,现代比赛用足球是由正五边形与正六边形构成的共32个面的多面体,著名数学家欧拉证明了凸多面体的面数(F),顶点数(V),棱数(E)满足F+V-E=2,那么,足球有______.个正六边形的面,若正六边形的边长为![]() ,则足球的直径为______.cm(结果保留整数)(参考数据
,则足球的直径为______.cm(结果保留整数)(参考数据![]()

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() ),它的上,下顶点分别为A,B,左,右焦点分别为
),它的上,下顶点分别为A,B,左,右焦点分别为![]() ,
,![]() ,若四边形
,若四边形![]() 为正方形,且面积为2.
为正方形,且面积为2.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)设存在斜率不为零且平行的两条直线![]() ,
,![]() ,它们与椭圆E分别交于点C,D,M,N,且四边形
,它们与椭圆E分别交于点C,D,M,N,且四边形![]() 是菱形,求出该菱形周长的最大值.
是菱形,求出该菱形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】个人所得税是国家对本国公民、居住在本国境内的个人的所得和境外个人来源于本国的所得征收的一种所得税.我国在1980年9月10日,第五届全国人民代表大会第三次会议通过并公布了《中华人民共和国个人所得税法》.公民依法诚信纳税是义务,更是责任现将自2013年至2017年的个人所得税收入统计如下

并制作了时间代号x与个人所得税收入的如如图所示的散点图:
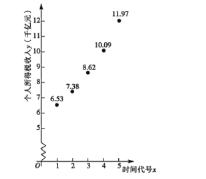
根据散点图判断,可用①y=menx与②![]() 作为年个人所得税收入y关于时间代号x的回归方程,经过数据运算和处理,得到如下数据:
作为年个人所得税收入y关于时间代号x的回归方程,经过数据运算和处理,得到如下数据:

以下计算过程中四舍五入保留两位小数.
(1)根据所给数据,分别求出①,②中y关于x的回归方程;
(2)已知2018年个人所得税收人为13.87千亿元,用2018年的数据验证(1)中所得两个回归方程,哪个更适宜作为y关于时间代号x的回归方程?
(3)你还能从统计学哪些角度来进一步确认哪个回归方程更适宜? (只需叙述,不必计算)
附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: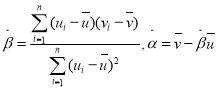
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的右焦点F为抛物线
的右焦点F为抛物线![]() 的焦点,点M为
的焦点,点M为![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
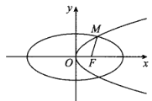
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,过焦点F的直线l与
,过焦点F的直线l与![]() 相交于A,B两点,已知
相交于A,B两点,已知![]() ,求
,求![]() 取得最大值时直线l的方程.
取得最大值时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com