
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系.
月份 |
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
【答案】(1)![]() ;(2)预测该商城8月份的销售额为126万元.
;(2)预测该商城8月份的销售额为126万元.
【解析】试题分析:(1)根据表格中所给数据及平均数公式可求出![]() 与
与![]() 的值从而可得样本中心点的坐标,求可得公式
的值从而可得样本中心点的坐标,求可得公式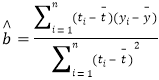 中所需数据,求出
中所需数据,求出![]() ,再结合样本中心点的性质可得
,再结合样本中心点的性质可得![]() ,进而可得
,进而可得![]() 关于
关于![]() 的回归方程;(2)由(1)知,
的回归方程;(2)由(1)知,![]() ,故前
,故前![]() 个月该淘宝商城月销售量逐月增加,平均每月增加
个月该淘宝商城月销售量逐月增加,平均每月增加![]() 万,将
万,将![]() ,代入(1)中的回归方程,可预测该商城
,代入(1)中的回归方程,可预测该商城![]() 月份的销售额.
月份的销售额.
.试题解析:(1)由所给数据计算得![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
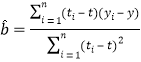
![]() ,
,![]()
![]() .
.
所求回归方程为![]() .
.
(2)由(1)知,![]() ,故前7个月该淘宝商城月销售量逐月增加,平均每月增加10万.
,故前7个月该淘宝商城月销售量逐月增加,平均每月增加10万.
将![]() ,代入(1)中的回归方程,得
,代入(1)中的回归方程,得![]() .
.
故预测该商城8月份的销售额为126万元.
【方法点晴】本题主要考查线性回归方程求法与实际应用,属于中档题. 求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ; 回归直线过样本点中心
; 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


科目:高中数学 来源: 题型:
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交的作品的件数按5天一组分组统计,绘制了频率分布直方图,如图所示,已知从左到右各长方形的高的比为2 : 3 : 4 : 6 : 4 :1,第三组的频数为12.

(1)求本次活动参加评比的作品的件数;
(2)哪组上交的作品数量最多,有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A , B , C的对边分别为a , b , c , cos ![]() =
= ![]() .
.
(1)求cosB的值;
(2)若 ![]() ,b=2
,b=2 ![]() ,求a和c的值.
,求a和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,直线
中,直线 ![]() 的参数方程为
的参数方程为  (
( ![]() 为参数).再以原点为极点,以
为参数).再以原点为极点,以 ![]() 正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系 ![]() 有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆 ![]() 的方程为
的方程为 ![]() .
.
(1)求圆 ![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() 、
、 ![]() ,若点
,若点 ![]() 的坐标为
的坐标为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程和相关系数r,分别得到以下四个结论:
① ![]() ②
② ![]()
③ ![]() ④
④ ![]()
其中,一定不正确的结论序号是( )
A.②③
B.①④
C.①②③
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程和相关系数r,分别得到以下四个结论:
① ![]() ②
② ![]()
③ ![]() ④
④ ![]()
其中,一定不正确的结论序号是( )
A.②③
B.①④
C.①②③
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市卫生防疫部门为了控制某种病毒的传染,提供了批号分别为 ![]() 的五批疫苗,供全市所辖的
的五批疫苗,供全市所辖的 ![]() 三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
(1)求三个区注射的疫苗批号中恰好有两个区相同的概率;
(2)记 ![]() 三个区选择的疫苗批号的中位数为X,求 X的分布列及期望.
三个区选择的疫苗批号的中位数为X,求 X的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() .计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
.计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com