
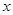 ,
, 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据:| 编号 | 1 | 2 | 3 | 4 | 5 |
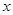 | 160 | 178 | 166 | 175 | 180 |
 | 75 | 80 | 77 | 70 | 81 |
 且
且 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数 的分布列及数学期望.
的分布列及数学期望.科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、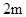 、
、 的钢管各
的钢管各 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根. 时,记事件
时,记事件 {抽取的
{抽取的 根钢管中恰有
根钢管中恰有 根长度相等},求
根长度相等},求 ;
; 时,若用
时,若用 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求 的分布列;
的分布列; ,
, ,求实数
,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com