Question

已知a＞1，在函数y=log_ax（x≥1）的图象上有A、B、C三点，它们的横坐标分别为t、t+2、t+4．
（1）若△ABC的面积为S，求S=f（t）；
（2）判断S=f（t）的单调性．

Answer 1

分析：（1）过A，B，C，分别作AA₁，BB₁，CC₁垂直于x轴，垂足为A₁，B₁，C₁，则S=S梯形AA₁B₁B+S梯形BB₁C₁C-S梯形AA₁C₁C，进而得出函数f（t）的表达式．
（2）由（1）中得f（t）=log2(1+

4

t2+4t

)，先根据 v＞1，推断v=t²+4t为增函数，进而推断函数f（t）为减函数．

解答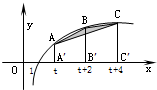：解：（1）过A，B，C，分别作AA₁，BB₁，CC₁垂直于x轴，垂足为A₁，B₁，C₁，
则S=S梯形AA₁B₁B+S梯形BB₁C₁C-S梯形AA₁C₁C

= 1 2 [logat+loga(t+2)]×2+ 1 2 [loga(t+2)+loga(t+4)]×2- 1 2 [logat+loga(t+4)]×4 =loga (t+2)2 t(t+4) =loga(1+ 4 t2+4t )

（2）因为v=t²+4t在[1，+∞）上是增函数，且v≥5，u=1+

4

v

在[5．+∞)上是减函数，且1＜u≤

9

5

；S=logau在(1，

9

5

]上是增函数，
所以复合函数S=f（t）=loga(1+

4

t2+4t

)在[1，+∞)上是减函数

点评：本题主要考查了函数单调性的应用．常涉及利用单调性求函数的值域和最值等问题．