
【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,S为△ABC的面积,![]() ,且A、B、C成等差数列,则C的大小为( )
,且A、B、C成等差数列,则C的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.

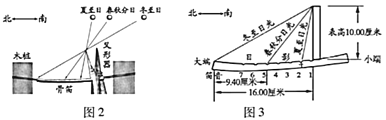
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点F的坐标为
右焦点F的坐标为![]() ,点
,点![]() 在椭圆C上,过F且斜率为
在椭圆C上,过F且斜率为![]() 的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
(I)求椭圆C的方程;
(Ⅱ)设线段AB的垂直平分线与x轴、y轴分别相交于点C,D.若![]() 与
与![]() 的面积相等,求直线l的斜率k.
的面积相等,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2013年至2019年新能源汽车y(单位:百台)的数据如下表:

(Ⅰ)求y关于x的线性回归方程,并预测该市2021年新能源汽车台数;
(Ⅱ)该市某公司计划投资600台“双枪同充”(两把充电枪)、“一拖四群充”(四把充电枪)的两种型号的直流充电桩.按要求,充电枪的总把数不少于该市2021年新能源汽车预测台数,若双枪同充、一拖四群充的每把充电枪的日利润分别为25元,10元,问两种型号的充电桩各安装多少台时,才能使日利润最大,求出最大日利润.![]()
附:回归直线的斜率和截距的最小二乘法估计公式分别为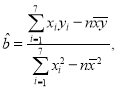
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2019年的高考考生人数是2016年高考考生人数的1.2倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考情况,得到如图柱状图:

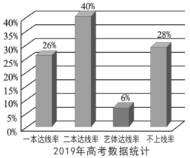
则下列结论正确的是( ).
A.与2016年相比,2019年不上线的人数有所增加
B.与2016年相比,2019年一本达线人数减少
C.与2016年相比,2019年二本达线人数增加了0.3倍
D.2016年与2019年艺体达线人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选题)下列说法中,正确的命题是( )
A.已知随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() .
.
B.以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
C.已知两个变量具有线性相关关系,其回归直线方程为![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
D.若样本数据![]() ,
,![]() ,…,
,…,![]() 的方差为2,则数据
的方差为2,则数据![]() ,
,![]() ,…,
,…,![]() 的方差为16.
的方差为16.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com