练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若“x∈[2，5]或x∈{x|x＜1或x＞4}”是假命题，则x的取值范围是 ．

    【答案】[1，2）
    【解析】解：若“x∈[2，5]或x∈{x|x＜1或x＞4}”是假命题 则它的否命题为真命题即{x|x＜2或x＞5}且{x|1≤x≤4}是真命题
    所以的取值范围是[1，2），
    所以答案是[1，2）．
    【考点精析】认真审题，首先需要了解元素与集合关系的判断(对象与集合的关系是，或者，两者必居其一)，还要掌握四种命题的真假关系(一个命题的真假与其他三个命题的真假有如下三条关系：(原命题 逆否命题)①、原命题为真，它的逆命题不一定为真;②、原命题为真，它的否命题不一定为真;③、原命题为真，它的逆否命题一定为真)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ax2﹣（a﹣1）x﹣lnx（a∈R且a≠0）．
    （1）求函数f（x）的单调递增区间；
    （2）记函数y=F（x）的图象为曲线C．设点A（x1 ， y1），B（x2 ， y2）是曲线C上的不同两点．如果在曲线C上存在点M（x0 ， y0），使得：①x0= ；②曲线C在点M处的切线平行于直线AB，则称函数F（x）存在“中值和谐切线”．当a=2时，函数f（x）是否存在“中值和谐切线”，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC的中点，F是DD1的中点，
    （1）求证：CF∥平面A1DE；
    （2）求二面角A1﹣DE﹣A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某辆汽车以x km/h的速度在高速公路上匀速行驶（考虑到高速公路行车安全要求60≤x≤120）时，每小时的油耗（所需要的汽油量）为，其中k为常数，若汽车以120km/h的速度行驶时，每小时的油耗为11.5L.

    （1）求k的值；

    （2）求该汽车每小时油耗的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正三棱柱ABC﹣A1B1C1中，已知AB=CC1=2，则异面直线AB1和BC1所成角的余弦值为（ ）
    A.0
    B.
    C.﹣
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元．该公司第n年需要付出设备的维修和工人工资等费用an的信息如图．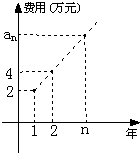

    （1）求an；
    （2）引进这种设备后，第几年后该公司开始获利；
    （3）这种设备使用多少年，该公司的年平均获利最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥D﹣ABC中，AB=BC=1，AD=2，BD= ，AC= ，BC⊥AD，则三棱锥的外接球的表面积为（ ）
    A. π
    B.6π
    C.5π
    D.8π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是空间两条直线， 是空间两个平面，则下列命题中不正确的是（ ）

    A. 当时，“”是“”的充要条件

    B. 当时，“”是“”的充分不必要条件

    C. 当时，“”是“”的必要不充分条件

    D. 当时，“”是“”的充分不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图平行四边形ABCD中，∠DAB=60°，AB=2，AD=2，M为CD边的中点，沿BM将△CBM折起使得平面BMC⊥平面ABMD．

    （1）求四棱锥C﹣ADMB的体积；
    （2）求折后直线AB与平面AMC所成的角的正弦．

    查看答案和解析>>

    同步练习册答案