
【题目】如图,点P、Q、R、S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的一个图是( )
A.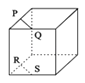
B.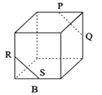
C.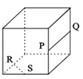
D.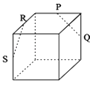
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 若对于任意的正整数n都有Sn=2an﹣3n.
(1)设bn=an+3,求证:数列{bn}是等比数列,并求出{an}的通项公式;
(2)求数列{nan}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南京一模19】设函数![]() ,
,![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记函数
时,记函数![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式
![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检.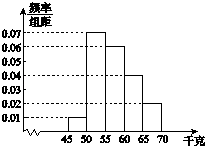
(1)求每组抽取的学生人数;
(2)若从6名学生中再次随机抽取2名学生进行复检,求这2名学生不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C(t, ![]() )(t∈R,t≠0)为圆心的圆过原点O.
)(t∈R,t≠0)为圆心的圆过原点O.
(1)设直线3x+y﹣4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(2)在(1)的条件下,设B(0,2),且P、Q分别是直线l:x+y+2=0和圆C上的动点,求|PQ|﹣|PB|的最大值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是首项为a1 , 公比为q的等比数列,Sn是{an}的前n项和.Sn= ![]() ;若am+an=as+at , 则m+n=s+t;Sk , S2k﹣Sk , S3k﹣S2k成等比数列(k∈N).
;若am+an=as+at , 则m+n=s+t;Sk , S2k﹣Sk , S3k﹣S2k成等比数列(k∈N).
以上说法正确的有( )个.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分14分)
在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是容量为100的样本的频率分布直方图,则样本数据在[6,10)内的频率和频数分别是( )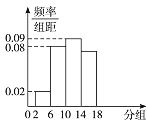
A.0.32,32
B.0.08,8
C.0.24,24
D.0.36,36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在过点(﹣5,﹣4)的直线l,使它与两坐标轴围成的三角形的面积为5?若存在,求出直线l的方程(化成直线方程的一般式);若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com