
| A. | $-\sqrt{3}≤u≤\sqrt{3}$ | B. | $u≥\sqrt{3}$或$u≤-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}≤u≤\frac{{\sqrt{3}}}{3}$ | D. | $u≥\frac{{\sqrt{3}}}{3}$或$u≤-\frac{{\sqrt{3}}}{3}$ |
分析 由题意得,点P(x,y)在圆C:x2+(y-1)2=1 上,而$u=\frac{y+1}{x}$表示圆上的点(x,y)与点M连线的斜率,如图,根据半径CA=1,MC=2,可得∠CMA=∠CMB=30°,可得MA的斜率和MB的斜率,从而求得μ的范围.
解答 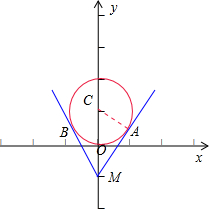 解:由题意可得,点P(x,y)在圆C:x2+(y-1)2=1 上,而$u=\frac{y+1}{x}$表示圆上的点(x,y)与点M(0,-1)连线的斜率,
解:由题意可得,点P(x,y)在圆C:x2+(y-1)2=1 上,而$u=\frac{y+1}{x}$表示圆上的点(x,y)与点M(0,-1)连线的斜率,
如图所示:
设MA MB和圆C相切,切点分别为A,B,由于半径CA=1,
MC=2,∴∠CMA=∠CMB=30°,
故MA的斜率为tan60°=$\sqrt{3}$,MB的斜率为tan(90°+30°)=-$\sqrt{3}$,
∴μ≥$\sqrt{3}$,或μ≤-$\sqrt{3}$,
故选:B.
点评 本题主要考查斜率公式、直线和圆的位置关系,体现了数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x>0,使得(x+1)ex>1” | B. | “x>0,总有(x+1)ex≥1” | ||
| C. | “x>0,使得(x+1)ex≤1” | D. | x>0,总有(x+1)ex<1” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
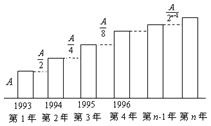 甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示:
甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com