
【题目】已知函数![]() .
.
(1)若![]() 都是从集合
都是从集合![]() 中任取的一个数,求函数
中任取的一个数,求函数![]() 有零点的概率;
有零点的概率;
(2)若![]() 都是从区间
都是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 成立的概率.
成立的概率.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛![]() 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛![]() ,要求
,要求![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上,且对角线
上,且对角线![]() 过
过![]() 点,已知
点,已知![]() 米,
米,![]() 米.
米.

(1)要使矩形![]() 的面积大于50平方米,则
的面积大于50平方米,则![]() 的长应在什么范围?
的长应在什么范围?
(2)当![]() 的长为多少米时,矩形花坛
的长为多少米时,矩形花坛![]() 的面积最小?并求出最小值.
的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(Ⅱ)利用(I)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1);

(Ⅲ)现要从医护专业知识考核分数95分以下的医护人员中选派2人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在90分以下的概率.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |

(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 中点,
中点,![]() ,
,![]() .现将
.现将![]() 沿
沿![]() 折起,如图2所示,使二面角
折起,如图2所示,使二面角![]() 为
为![]() ,
,![]() 是
是![]() 的中点.
的中点.
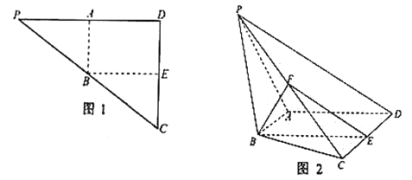
(1)求证:面![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为 ![]() ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为 ![]() ,猜对第3条的概率为
,猜对第3条的概率为 ![]() .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知海岛![]() 在海岛
在海岛![]() 北偏东
北偏东![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物体甲从海岛
海里,物体甲从海岛![]() 以
以![]() 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛![]() 移动,同时物体乙从海岛
移动,同时物体乙从海岛![]() 沿着海岛
沿着海岛![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小时的速度移动.
海里/小时的速度移动.
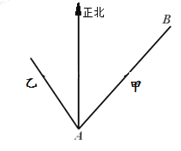
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛![]() 到达海岛
到达海岛![]() 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com