
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上的最大值和最小值的和为1,求实数
上的最大值和最小值的和为1,求实数![]() 的值.
的值.
【答案】(1)答案见解析.(2)![]()
【解析】
(1)利用![]() 的导函数
的导函数![]() ,求得
,求得![]() 的单调区间.
的单调区间.
(2)利用![]() 的导函数
的导函数![]() ,求得
,求得![]() 的单调区间,对
的单调区间,对![]() 分成
分成![]() ,
,![]() ,
,![]() 三种情况进行分类讨论,结合
三种情况进行分类讨论,结合![]() 在区间
在区间![]() 上最大值和最小的和为
上最大值和最小的和为![]() ,求得实数
,求得实数![]() 的值.
的值.
(1)当a=3时,f(x)=2x3﹣3x2+1,x∈R,
∴f'(x)=6x2﹣6x=6x(x﹣1),
令f'(x)>0得,x<0或x>1;令f'(x)<0得,0<x<1,
∴函数f(x)的的单调增区间为(﹣∞,0)和(1,+∞),单调递减区间为(0,1),
(2)函数f(x)=2x3﹣ax2+1,a>0,
∴f'(x)=6x2﹣2ax=2x(3x﹣a),
令f'(x)=0得,x=0或![]() ,
,
列表:
x | (﹣∞,0) | 0 | (0, |
| ( |
f'(x) | + | 0 | ﹣ | 0 | + |
f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
①当0<a≤2时,0![]() ,
,
∴函数f(x)在[﹣1,0]上单调递增,在[0,![]() ]上单调递减,在[
]上单调递减,在[![]() ,1]上单调递增,
,1]上单调递增,
又∵f(﹣1)=﹣1﹣a,f(0)=1,f(1)=3﹣a≥1,f(![]() )=1
)=1![]() ,且0<f(
,且0<f(![]() )<1,
)<1,
∴f(x)max=f(1)=3﹣a,f(x)min=f(﹣1)=﹣1﹣a,
∴(3﹣a)+(﹣1﹣a)=1,
∴a![]() ,
,
②当2<a<3时,0![]() ,
,
∴函数f(x)在[﹣1,0]上单调递增,在[0,![]() ]上单调递减,在[
]上单调递减,在[![]() ,1]上单调递增,
,1]上单调递增,
又∵f(﹣1)=﹣1﹣a,f(0)=1,f(1)=3﹣a,f(![]() )=1
)=1![]() ,且0<f(
,且0<f(![]() )<1,0<f(1)<1,
)<1,0<f(1)<1,
∴f(x)max=f(0)=1,f(x)min=f(﹣1)=﹣1﹣a,
∴1+(﹣1﹣a)=1,
∴a=﹣1,不符合题意,舍去,
③当a≥3时,![]() ,
,
∴函数f(x)在[﹣1,0]上单调递增,在[0,1]上单调递减,
∴f(x)max=f(0)=1,
又∵f(﹣1)=﹣1﹣a,f(1)=3﹣a,∴f(x)min=f(﹣1)=﹣1﹣a,
∴1+(﹣1﹣a)=1,
∴a=﹣1,不符合题意,舍去,
综上所述,若函数f(x)在[﹣1,1]上的最大值和最小值的和为1,实数a的值为![]() .
.


科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓后要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现三次音乐获得150分,出现两次音乐获得100分,出现一次音乐获得50分,没有出现音乐则获得-300分.设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)若一盘游戏中仅出现一次音乐的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() ;
;
(2)以(1)中确定的![]() 作为
作为![]() 的值,玩3盘游戏,出现音乐的盘数为随机变量
的值,玩3盘游戏,出现音乐的盘数为随机变量![]() ,求每盘游戏出现音乐的概率
,求每盘游戏出现音乐的概率![]() ,及随机变量
,及随机变量![]() 的期望
的期望![]() ;
;
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x![]() |(a>0).
|(a>0).
(1)若不等式f(x)﹣| x![]() |≥4x的解集为{x|x≤1},求实数a的值;
|≥4x的解集为{x|x≤1},求实数a的值;
(2)证明:f(x)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,短轴长为2,过定点
,短轴长为2,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间).
之间).
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若射线![]() 交椭圆
交椭圆![]() 于点
于点![]() (
(![]() 为原点),求
为原点),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是曲线
是曲线![]() :
:![]() (
(![]() 为参数)上的动点,以坐标原点
为参数)上的动点,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,以极点
轴的正半轴为极轴建立极坐标系,以极点![]() 为中心,将线段
为中心,将线段![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() 的坐标为
的坐标为![]() ,射线
,射线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.

(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为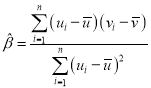 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com