
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数 ![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)求证:  (
(![]() ,
, ![]() 是自然对数的底数).
是自然对数的底数).
【答案】(Ⅰ)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅱ)
;(Ⅱ)![]() ; (Ⅲ)见解析.
; (Ⅲ)见解析.
【解析】分析:(Ⅰ)求出函数的导数,分别解不等式![]() 、
、![]() ,可求得
,可求得![]() 的增区间和减区间.
的增区间和减区间.
(Ⅱ)构建新函数![]() , 不等式
, 不等式![]() 在
在![]() 上恒成立等价于
上恒成立等价于![]() 在
在![]() 恒成立,而
恒成立,而![]() ,分
,分![]() 三种情形讨论可得实数
三种情形讨论可得实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅲ)由(Ⅱ)得不等式![]() ,
, ![]() ,故有
,故有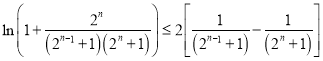 ,利用累加及其裂项相消法可以得到:
,利用累加及其裂项相消法可以得到: 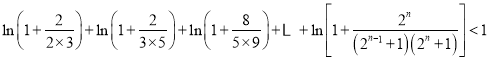 ,化简后可得到要证明的不等式.
,化简后可得到要证明的不等式.
详解:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]() .
.
由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)因当![]() 时,不等式
时,不等式![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
设![]() ,只需
,只需![]() 即可.
即可.
由![]() ,
,
(ⅰ)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
故![]() 成立;
成立;
(ⅱ)当![]() 时,由
时,由![]() ,因
,因![]() ,所以
,所以![]() ,
,
①若![]() ,即
,即![]() 时,在区间
时,在区间![]() 上,
上, ![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 在
在![]() 上无最大值;
上无最大值;
②若![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,同样
上单调递增,同样![]() 在
在![]() 上无最大值,不满足条件;
上无最大值,不满足条件;
(ⅲ)当![]() 时,由
时,由![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,故函数
,故函数![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 成立.
成立.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)据(Ⅱ)知当![]() 时,
时, ![]() 在
在![]() 上恒成立,又
上恒成立,又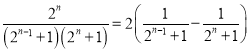 ,
,
∵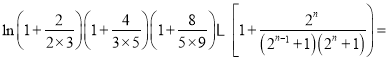
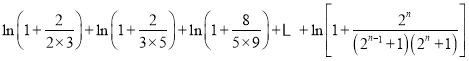
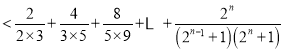
![]() ,
,
∴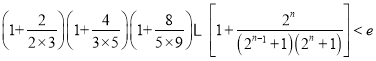 .
.


科目:高中数学 来源: 题型:
【题目】已知某种药物在血液中以每小时![]() 的比例衰减,现给某病人静脉注射了该药物2500mg,设经过x个小时后,药物在病人血液中的量为ymg.
的比例衰减,现给某病人静脉注射了该药物2500mg,设经过x个小时后,药物在病人血液中的量为ymg.
![]() 与x的关系式为______;
与x的关系式为______;
![]() 当该药物在病人血液中的量保持在1500mg以上,才有疗效;而低于500mg,病人就有危险,要使病人没有危险,再次注射该药物的时间不能超过______小时
当该药物在病人血液中的量保持在1500mg以上,才有疗效;而低于500mg,病人就有危险,要使病人没有危险,再次注射该药物的时间不能超过______小时![]() 精确到
精确到![]() .
.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在圆x2+y2﹣4x+2y=0内,过点E(1,0)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )
A.![]()
B.6 ![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且过定点M(1,
,且过定点M(1, ![]() ).
).
(1)求椭圆C的方程;
(2)已知直线l:y=kx﹣ ![]() (k∈R)与椭圆C交于A、B两点,试问在y轴上是否存在定点P,使得以弦AB为直径的圆恒过P点?若存在,求出P点的坐标和△PAB的面积的最大值,若不存在,说明理由.
(k∈R)与椭圆C交于A、B两点,试问在y轴上是否存在定点P,使得以弦AB为直径的圆恒过P点?若存在,求出P点的坐标和△PAB的面积的最大值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线l的参数方程 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为p2cos2θ+p2sinθ﹣2psinθ﹣3=0
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为p2cos2θ+p2sinθ﹣2psinθ﹣3=0
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题是![]()
![]()
A. 任意三点确定一个平面
B. 三条平行直线最多确定一个平面
C. 不同的两条直线均垂直于同一个平面,则这两条直线平行
D. 一个平面中的两条直线与另一个平面都平行,则这两个平面平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列四个命题:
![]() 若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
![]() 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
![]() 垂直于同一直线的两条直线相互平行;
垂直于同一直线的两条直线相互平行;
![]() 若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是![]()
![]()
A. ![]() 和
和![]() B.
B. ![]() 和
和![]() C.
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com