
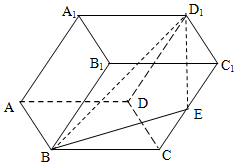
 已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,
已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,分析 (1)延长AD,过D1作D1H⊥AD于H,连结BH,可得∠D1BH为直线BD1与平面ABCD所成的角,
(2)取AD中点O,即AO⊥面ABCD.故如图建立空间直角坐标系O=xyz.要使得MB1⊥平面BED1,则$\left\{\begin{array}{l}{\overrightarrow{M{B}_{1}}•\overrightarrow{B{D}_{1}}=0}\\{\overrightarrow{M{B}_{1}}•\overrightarrow{BE}=0}\end{array}\right.$,$\left\{\begin{array}{l}{3x-1+3=0}\\{\frac{5}{2}x+\frac{3}{2}=0}\end{array}\right.$,方程组无解.
即在线段AD上不存在一点M,使得MB1⊥平面BED1
解答 解:(1):延长AD,过D1作D1H⊥AD于H,连结BH,
因为平面A1ADD1⊥平面ABCD,平面A1ADD1∩平面ABCD=AD,
所以D1H⊥平面ABCD,即BH为BD1在平面ABCD内的射影,
所以∠D1BH为直线BD1与平面ABCD所成的角,
因为D1H=2sin60°=$\sqrt{3}$.
BH=$\sqrt{A{B}^{2}+A{E}^{2}}=\sqrt{13}$,D1B=4
所以,sin∠D1BH=$\frac{\sqrt{3}}{4}$
∴直线BD1与平面ABCD所成的角的正弦值为$\frac{\sqrt{3}}{4}$;
(2)取AD中点O,
∵四棱柱平面ABCD-A1B1C1D1的各棱长均为2,
∠A1AD=60°,∴AO⊥AD.
又∵平面A1ADD1⊥平面ABCD,∴AO⊥面ABCD.
故如图建立空间直角坐标系O=xyz.
则O(0,0,0),A(1,0,0),D1(-2,O,$\sqrt{3}$),
C(-1,1,0),C1(-2,1,$\sqrt{3}$)B1(0,1,$\sqrt{3}$)
设M(x,0,0).则$\overrightarrow{M{B}_{1}}=(-x,1,\sqrt{3})$,$\overrightarrow{B{D}_{1}}=(-3,-1,\sqrt{3}),\overrightarrow{BE}=(-\frac{5}{2},0,\frac{\sqrt{3}}{2})$,
要使得MB1⊥平面BED1,则$\left\{\begin{array}{l}{\overrightarrow{M{B}_{1}}•\overrightarrow{B{D}_{1}}=0}\\{\overrightarrow{M{B}_{1}}•\overrightarrow{BE}=0}\end{array}\right.$,$\left\{\begin{array}{l}{3x-1+3=0}\\{\frac{5}{2}x+\frac{3}{2}=0}\end{array}\right.$,方程组无解.
∴在线段AD上不存在一点M,使得MB1⊥平面BED1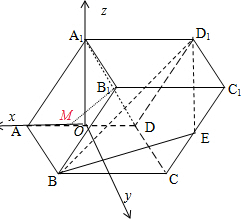
点评 本题考查了空间线面角的求解,动点存在性问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (2,-$\frac{π}{3}$) | B. | (2,$\frac{4π}{3}$) | C. | (2,$\frac{π}{3}$) | D. | (2,-$\frac{4π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{9}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有95%的把握认为两者有关 | B. | 约有95%的打鼾者患心脏病 | ||
| C. | 有99%的把握认为两者有关 | D. | 约有95%的打鼾者患心脏病 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com