
【题目】△ABC中,角A,B,C所对边分别为a,b,c,a=2,B=45°,①当b= ![]() 时,三角形有个解;②若三角形有两解,则b的取值范围是 .
时,三角形有个解;②若三角形有两解,则b的取值范围是 .
【答案】1;(2,2 ![]() )
)
【解析】解:①∵△ABC中,角A,B,C所对边分别为a,b,c, a=2,B=45°,b= ![]() ,
,
由正弦定理 ![]() ,得
,得 ![]() ,
,
解得sinA=1,∴A=90°,三角形只有一个解.
所以答案是:1.
②BC=a=2,要使三角形有两解,就是要使以C为圆心,半径为2的圆与BA有两个交点,
当A=90°时,圆与AB相切;
当A=45°时交于B点,也就是只有一解,
∴45°<A<90°,即 ![]() <sinA<1,
<sinA<1,
由正弦定理以及asinB=bsinA.可得:b=x= ![]() =2
=2 ![]() sinA,
sinA,
∵2 ![]() sinA∈(2,2
sinA∈(2,2 ![]() ).
).
∴b的取值范围是(2,2 ![]() ).
).
所以答案是:(2,2 ![]() ).
).
【考点精析】认真审题,首先需要了解正弦定理的定义(正弦定理:![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交 ![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.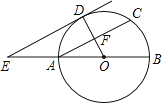
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三文科500名学生参加了5月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,抽出的100名学生的数学、语文成绩如下表:

(1)将学生编号为:001,002,003,……,499,500.若从第5行第5列的数开始右读,请你依次写出最先抽出的5个人的编号(下面是摘自随机数表的第4行至第7行)

(2)若数学的优秀率为![]() ,求
,求![]() 的值;
的值;
(3)在语文成绩为良好的学生中,已知![]() ,求数学成绩“优”比“良”的人数少的概率.
,求数学成绩“优”比“良”的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是等差数列,前n项和为Sn , {bn}是单调递增的等比数列,b1=2是a1与a2的等差中项,a3=5,b3=a4+1,若当n≥m时,Sn≤bn恒成立,则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对边分别为a,b,c,已知 ![]() . (Ⅰ)若b=
. (Ⅰ)若b= ![]() ,当△ABC周长取最大值时,求△ABC的面积;
,当△ABC周长取最大值时,求△ABC的面积;
(Ⅱ)设 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届湖南省长沙市高三上学期统一模拟考试文数】已知过![]() 的动圆恒与
的动圆恒与![]() 轴相切,设切点为
轴相切,设切点为![]() 是该圆的直径.
是该圆的直径.
(Ⅰ)求![]() 点轨迹
点轨迹![]() 的方程;
的方程;
(Ⅱ)当![]() 不在y轴上时,设直线
不在y轴上时,设直线![]() 与曲线
与曲线![]() 交于另一点
交于另一点![]() ,该曲线在
,该曲线在![]() 处的切线与直线
处的切线与直线![]() 交于
交于![]() 点.求证:
点.求证: ![]() 恒为直角三角形.
恒为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,角
中,角![]() ,
,![]() ,
,![]() 所对的边分别是
所对的边分别是![]() ,
,![]() ,
,![]() ,且点
,且点![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() (
(![]() 为常数且
为常数且![]() ),动点
),动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)试求曲线![]() 的方程;
的方程;
(Ⅱ)当![]() 时,过定点
时,过定点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 是曲线
是曲线![]() 上不同于
上不同于![]() ,
,![]() 的动点,试求
的动点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com