
【题目】在二项式(axm+bxn)12(a>0,b>0,m、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项.
(1)求它是第几项;
(2)求 ![]() 的范围.
的范围.
【答案】
(1)解:设Tr+1=C12r(axm)12﹣r(bxn)r=C12ra12﹣rbrxm(12﹣r)+nr为常数项,
则有m(12﹣r)+nr=0,即m(12﹣r)﹣2mr=0,∴r=4,它是第5项
(2)解:∵第5项又是系数最大的项,
∴有 ![]()
由①得a8b4≥ ![]() a9b3,
a9b3,
∵a>0,b>0,∴ ![]() b≥a,即
b≥a,即 ![]() ≤
≤ ![]() .
.
由②得 ![]() ≥
≥ ![]() ,
,
∴ ![]() ≤
≤ ![]() ≤
≤ ![]()
【解析】(1)利用二项展开式的通项公式确定出展开式中的常数项是第几项是解决本小题的关键;(2)通过系数最大列出关于a,b的不等式,通过整体思想确定出 ![]() 的范围.蕴含了不等式思想.
的范围.蕴含了不等式思想.
【考点精析】本题主要考查了二项式定理的通项公式的相关知识点,需要掌握二项式通项公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且S4=4S2 , a2n=2an+1.
(Ⅰ)求数列{an}的通项公式
(Ⅱ)设数列{bn}的前n项和为Tn , 且 ![]() (λ为常数).令cn=b2n , (n∈N*),求数列{cn}的前n项和Rn .
(λ为常数).令cn=b2n , (n∈N*),求数列{cn}的前n项和Rn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)用定义证明函数f(x)在(﹣∞,+∞)上为减函数;
(2)若x∈[1,2],求函数f(x)的值域;
(3)若g(x)= ![]() ,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围.
,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() ,其导函数为
,其导函数为![]() ,若对任意的实数
,若对任意的实数![]() ,都有
,都有![]() 恒成立,则使
恒成立,则使![]() 成立的实数
成立的实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1的侧面ACC1A1是正方形,AC=BC,点O是侧面ACC1A1的中心,∠ACB= ![]() ,M在棱BC上,且MC=2BM=2.
,M在棱BC上,且MC=2BM=2. 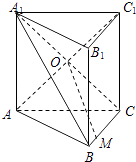
(1)证明BC⊥AC1;
(2)求OM的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (b≠0且b是常数).
(b≠0且b是常数).
(1)如果方程f(x)=x有唯一解,求b值.
(2)在(1)的条件下,求证:f(x)在(﹣∞,﹣1)上是增函数;
(3)若函数f(x)在(1,+∞)上是减函数,求负数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在10件产品中,有2件一等品,4件二等品,4件三等品,从这10件产品中任取3件,求
(1)取出的3件产品中一等品件数X的分布列和数学期望;
(2)取出的3件产品中至多有1件一等品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com