设向量
，
，其中s,t为不同时为0的两个实数，实数
，满足
。
（1）求函数关系S=F
;
(2) 若F在（1，+∞）上单调递增，求实数
的取值范围；
（3）对于上述F，当=0时，存在正数列{
n},满足F
+F
+……+F
=
²，其中
，求证：
名校课堂系列答案科目：高中数学 来源： 题型：
设平面上的动向量
，
，其中s、t为不同时为0的两个实数，实数
，满足
。
（1）求函数关系式
；
（2）若函数
在
上单调递增，求
的范围；
（3）对上述，当
时，存在正项数列
满足
，其中
，证明：
。
查看答案和解析>>
科目：高中数学 来源：四川省雅安中学09-10学年高二上学期九月月考 题型：解答题
设向量
，
，其中s,t为不同时为0的两个实数，实数
，满足
。
（1）求函数关系S=F
;
(2) 若F在（1，+∞）上单调递增，求实数
的取值范围；
（3）对于上述F，当=0时，存在正数列{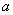
n},满足F
+F
+……+F
=
²，其中
，求证：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，所以
³
成立
=
又
=
两式相减
两式相减
，所以数列{
}是公差为1的等差数列。
，得
=
=
满足
，
，且
的模分别为s，t，其中s=
=1，t=
,
则
的模为__
_