练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增，则满足不等式f（1）＜f（lg ）的x的取值范围是 ．

    【答案】（0,1）∪（100,+∞）
    【解析】解：∵函数f（x）是定义在R上的偶函数，∴f（1）＜f（lg ）=f（|lg |）

    ∵函数f（x）在区间[0，+∞）上单调递增，∴|lg |＞1，即lg ＞1或lg ＜﹣1解得：x＞100或0＜x＜1

    所以满足不等式f（1）＜f（lg ）的x的取值范围是（0，1）∪（100，+∞）．

    所以答案是：（0，1）∪（100，+∞）．

    【考点精析】掌握奇偶性与单调性的综合是解答本题的根本，需要知道奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设{ an}为等比数列，{bn}为等差数列，且b1=0，cn=an+bn ， 若{ cn}是1，1，2，…，求数列{ cn}的前10项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数 的图象为C，则如下结论中正确的是（写出所有正确结论的编号）．
    ①图象C关于直线 对称；
    ②图象C关于点 对称；
    ③函数f（x）在区间 内是减函数；
    ④把函数 的图象上点的横坐标压缩为原来的一半（纵坐标不变）可以得到图象C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】欧巴老师布置给时镇同学这样一份数学作业：在同一个直角坐标系中画出四个对数函数的图象，使它们的底数分别为 和 ．时镇同学为了和暮烟同学出去玩，问大英同学借了作业本很快就抄好了，详见如图．第二天，欧巴老师当堂质问时镇同学：“你画的四条曲线中，哪条是底数为e的对数函数图象？”时镇同学无言以对，憋得满脸通红，眼看时镇同学就要被欧巴老师训斥一番，聪明睿智的你能不能帮他一把，回答这个问题呢？曲线才是底数为e的对数函数的图象．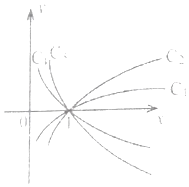

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x，y的方程C：x2+y2﹣2x﹣4y+m=0
    （1）当方程C表示圆时，求m的取值范围；
    （2）若圆C与直线l1：x+2y﹣4=0相交于M，N两点，且|MN|= ，求m的值；
    （3）在（2）条件下，若圆C上存在四点到直线l2：x﹣2y+b=0的距离均为 ，试求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知α∈（0， ），β∈（0， ），且满足 cos2 + sin2 = + ，sin（2017π﹣α）= cos（ π﹣β），则α+β= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，记正方形ABCD四条边的中点为S，M，N，T，连接四个中点得小正方形SMNT．将正方形ABCD，正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1 ， V2 ， 则V1：V2=（ ）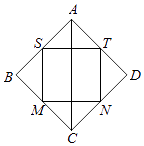

    A.8：1
    B.2：1
    C.4：3
    D.8：3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）= x﹣lnx（x＞0），则函数f（x）（ ）
    A.在区间（0，1）内有零点，在区间（1，+∞）内无零点
    B.在区间（0，1）内有零点，在区间（1，+∞）内有零点
    C.在区间（0，3），（3，+∞）均无零点
    D.在区间（0，3），（3，+∞）均有零点

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等差数列{an}中，a1=1，前n项和Sn满足条件 =4，n=1，2，…
    （1）求数列{an}的通项公式和Sn；
    （2）记bn= ，求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    同步练习册答案