
【题目】已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=﹣1时,求f(x)的最大值;
(2)若f(x)在区间(0,e]上的最大值为﹣3,求a的值;
(3)设g(x)=xf(x),若a>0,对于任意的两个正实数x1 , x2(x1≠x2),证明:2g( ![]() )<g(x1)+g(x2).
)<g(x1)+g(x2).
【答案】
(1)解:易知f(x)定义域为(0,+∞),
当a=﹣1时,f(x)=﹣x+lnx, ![]() ,
,
令f′(x)=0,得x=1.
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0,
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
f(x)max=f(1)=﹣1.
∴函数f(x)在(0,+∞)上的最大值为﹣1
(2)解:∵ ![]() .
.
①若 ![]() ,则f′(x)≥0,从而f(x)在(0,e]上是增函数,
,则f′(x)≥0,从而f(x)在(0,e]上是增函数,
∴f(x)max=f(e)=ae+1≥0,不合题意,
②若 ![]() ,则由
,则由 ![]() ,即
,即 ![]()
由 ![]() ,即
,即 ![]() ,
,
从而f(x)在(0,﹣ ![]() )上增函数,在(﹣
)上增函数,在(﹣ ![]() ,e]为减函数
,e]为减函数
∴ ![]()
令 ![]() ,则
,则 ![]() ,
,
∴a=﹣e2
(3)证明:∵g(x)=xf(x)=ax2+xlnx,x>0
∴ ![]() ,
,
∴g′(x)为增函数,不妨令x2>x1
令 ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]()
而h(x1)=0,知x>x1时,h(x)>0
故h(x2)>0,
即 ![]()
【解析】(1)在定义域(0,+∞)内对函数f(x)求导,求其极大值,若是唯一极值点,则极大值即为最大值.(2)在定义域(0,+∞)内对函数f(x)求导,对a进行分类讨论并判断其单调性,根据f(x)在区间(0,e]上的单调性求其最大值,并判断其最大值是否为﹣3,若是就可求出相应的最大值.(3)先求导,再求导,得到g′(x)为增函数,不妨令x2>x1 , 构造函数 ![]() ,利用导数即可证明
,利用导数即可证明


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】下列命题中的假命题是( )
A.x0∈(0,+∞),x0<sinx0
B.x∈(﹣∞,0),ex>x+1
C.x>0,5x>3x
D.x0∈R,lnx0<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
(Ⅰ)求图中x的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;
(Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制,再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历,记这3名志愿者中年龄不低于35岁的人数为X,求X的分布列及数学期望.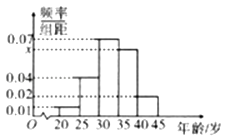
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确是 , (写出所有正确命题的序号)
①若奇函数f(x)的周期为4,则函数f(x)的图象关于(2,0)对称;
②若a∈(0,1),则a1+a<a ![]() ;
;
③函数f(x)=ln ![]() 是奇函数;
是奇函数;
④存在唯一的实数a使f(x)=lg(ax+ ![]() )为奇函数.
)为奇函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点的坐标为A(0,1),B(1,0),C(0,﹣2),O为坐标原点,动点M满足| ![]() |=1,则|
|=1,则| ![]() +
+ ![]() +
+ ![]() |的最大值是( )
|的最大值是( )
A.![]()
B.![]()
C.![]() ﹣1
﹣1
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线的顶点在坐标原点,焦点F在y轴正半轴上,过点F的直线交抛物线于A,B两点,线段AB的长是8,AB的中点到x轴的距离是3.
(1)求抛物线的标准方程;
(2)设直线m在y轴上的截距为6,且与抛物线交于P,Q两点,连结QF并延长交抛物线的准线于点R,当直线PR恰与抛物线相切时,求直线m的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴非负半轴重合,直线l的参数方程为:  (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)设直线l与曲线C相交于P,Q两点,求|PQ|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com