
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),其中
为参数),其中![]() .
. ![]() 与
与![]() 交于点
交于点![]() ,求直线
,求直线![]() 的斜率.
的斜率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
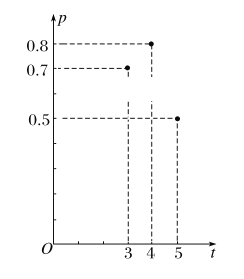
【题目】加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系![]() (a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为________分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年,在国家创新驱动战略下,北斗系统作为一项国家高科技工程,一个开放型的创新平台,1400多个北斗基站遍布全国,上万台套设备组成星地“一张网”,国内定位精度全部达到亚米级,部分地区达到分米级,最高精度甚至可以达到厘米或毫米级。最近北斗三号工程耗资9万元建成一小型设备,已知这台设备从启用的第一天起连续使用,第![]() 天的维修保养费为
天的维修保养费为![]() 元,使用它直至“报废最合算”(所谓“报废最合算”是指使用这台仪器的平均每天耗资最少)为止,一共使用了多少天,平均每天耗资多少钱?
元,使用它直至“报废最合算”(所谓“报废最合算”是指使用这台仪器的平均每天耗资最少)为止,一共使用了多少天,平均每天耗资多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2017年某交社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们的年龄分成6组![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
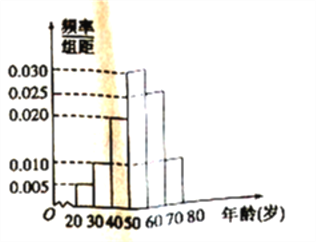
(1)根据广场舞者年龄的频率分布直方图,估计广场舞者的平均年龄;
(2)若从年龄在![]() 内的广场舞者中任取2名,求选中的两人中至少有一人年龄在
内的广场舞者中任取2名,求选中的两人中至少有一人年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格![]() (单位:元)与销售时间
(单位:元)与销售时间![]() (单位:天)的函数关系为
(单位:天)的函数关系为![]() ,
,![]() ,且该商品的日销售量Q(单位:件)与销售时间
,且该商品的日销售量Q(单位:件)与销售时间![]() (单位:天)的函数关系为
(单位:天)的函数关系为![]() ,则这种商品的日销售量金额最大的一天是30天中的第__________天.
,则这种商品的日销售量金额最大的一天是30天中的第__________天.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为
为![]() 的倾斜角).以坐标原点为极点,
的倾斜角).以坐标原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系.曲线
轴的正半轴为极轴,建立极坐标系.曲线![]() ,曲线
,曲线![]() .
.
(1)若直线与![]() 有且仅有一个公共点,求直线
有且仅有一个公共点,求直线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,与
,与![]() 交于不同两点
交于不同两点![]() ,这四点从左到右依次为
,这四点从左到右依次为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com