
 ����֪����aȡ��ͬ��ֵʱ���õ���ͬ�����У��統a=1ʱ���õ��������У�1��2��
����֪����aȡ��ͬ��ֵʱ���õ���ͬ�����У��統a=1ʱ���õ��������У�1��2�� ��
�� ������a=-
������a=- ʱ���õ��������У�-
ʱ���õ��������У�- ��-1��0��
��-1��0��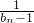 ��n��N+������֤aȡ����{bn}�е���һ�����������Եõ�һ����������{an}��
��n��N+������֤aȡ����{bn}�е���һ�����������Եõ�һ����������{an}�� ��an��2��n��4������a��ȡֵ��Χ��
��an��2��n��4������a��ȡֵ��Χ�� ����an=
����an= ����a4=0����a3=-1��a2=-
����a4=0����a3=-1��a2=- ��a=a1=-
��a=a1=- ��
�� ����a2=
����a2= ��a3=
��a3=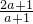 ��a4=
��a4= ����a4=0����a=-
����a4=0����a=- ��
��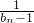 ����bn=
����bn= +1��
+1�� =1+
=1+ =bn-1��a3=1+
=bn-1��a3=1+ =1+
=1+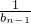 =bn-2��
=bn-2�� =0
=0 ��an��2��n��4��?
��an��2��n��4��? ��n��5��?
��n��5��? ?
? ��an-1��2��n��5��
��an-1��2��n��5�� ��an��2��n��4��?
��an��2��n��4��? ��a4��2?
��a4��2? ��
�� ��2?a��0
��2?a��0 ����a4=0������a3=-1����������a2=-
����a4=0������a3=-1����������a2=- ���ɴ˿�֪a=a1=-
���ɴ˿�֪a=a1=- ��
�� �������Ƶ���a4=
�������Ƶ���a4= 0���ɴ˿�֪a=-
0���ɴ˿�֪a=- ��
��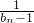 ��֪bn=
��֪bn= +1����a=bn���������������ܹ��Ƴ�an=1+
+1����a=bn���������������ܹ��Ƴ�an=1+ =0��������{an}ֻ����n��Ϊ�������У�
=0��������{an}ֻ����n��Ϊ�������У� ��n��5�����ɴ��ܹ��Ƴ�a��ȡֵ��Χ��
��n��5�����ɴ��ܹ��Ƴ�a��ȡֵ��Χ��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3+4an |
| 12-4an |
| 1 | ||
an-
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 5 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com