练习册

  • 练习册
  • 试题
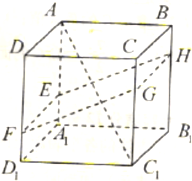    精英家教网 > 高中数学 > 题目详情
    如图13，EFGH的四个顶点分别在空间四边形ABCD的边AB、BC、CD、DA上，求证：BD∥面EFGH，AC∥面EFGH.

    证明：∵四边形EFGH是平行四边形

    图13

    BD∥面EFGH.

    同理,可证AC∥面EFGH.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，正方体AC1中，
    DF
    DD1
    =
    AE
    AA1
    =
    2
    3
    ，
    CG
    CC1
    =
    BH
    BB1
    =
    1
    3
    ，点P为平面EFGH内的一动点，且满足∠PAA1=∠C1AA1，则点P的轨迹是（　　）
    A、抛物线B、圆C、椭圆D、双曲线

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分13分）

    某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.

    （1）请画出该安全标识墩的侧(左)视图;

    （2）求该安全标识墩的体积

    （3）证明：直线BD平面PEG

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    .(2009年广东卷文)（本小题满分13分）

    某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.

    （1）请画出该安全标识墩的侧(左)视图;

    （2）求该安全标识墩的体积

    （3）证明:直线BD平面PEG

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图13,在正方体ABCD—EFGH中，M、N、P、Q、R分别是EH、EF、BC、CD、AD的中点，求证：平面MNA∥平面PQG.

    图13

    查看答案和解析>>

    同步练习册答案