
| A. | (-2,0] | B. | (0,2] | C. | (-∞,4] | D. | [4,+∞) |
分析 求出f(x),g(x)的值域,则f(x)的值域为g(x)的值域的子集.
解答 解:f(x)=-|x|≤0,∴f(x)的值域是(-∞,0].设g(x)的值域为A,
∵对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),
∴(-∞,0]⊆A.
设y=ax2-4x+1的值域为B,
则(0,1]⊆B.
由题意当a=0时,上式成立.
当a>0时,△=16-4a≥0,解得0<a≤4.
当a<0时,ymax=$\frac{4a-16}{4a}$≥1,即1-$\frac{4}{a}$≥1恒成立.
综上,a≤4.
故选:C.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意对数性质的合理运用.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
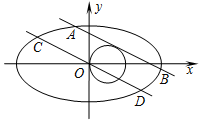 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,且过点$({2,\sqrt{3}}))$,直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,3,4} | B. | {0,1} | C. | {0,1,4} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{7π}{12},0)$ | B. | $(\frac{π}{6},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{2π}{3},-3)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
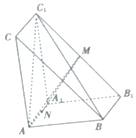 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com