Question

7．三角形与四面体有着类似的特征．如图1，△ABC中，若AD是∠BAC的角平分线，则$\frac{DB}{DC}=\frac{AB}{AC}$．依此类比：如图2，三棱锥S-PQR中，点M在QR上，若二面角Q-SP-M的大小等于二面角R-SP-M的大小，则$\frac{MQ}{MR}$=$\frac{{S}_{△PSQ}}{{S}_{△PSR}}$．

Answer 1

分析 将类比中的情景置于特殊情况之中，据此得出“类比结论”，这是解此类问题的常用方法．

解答 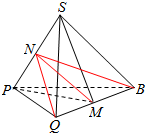解：不妨设QP=QS，RP=RS，
再取PS的中点N，则QN⊥PS，RN⊥PS，如右图：
因为，△SQR≌△PQR，所以，MP=MS，
所以，MN⊥PS，因此根据几何关系可知，
二面角Q-SP-M的平面角为：∠QNM，
二面角R-SP-M的平面角为：∠RNM，
因为以上两个二面角角的平面相等，即∠QNM=∠RNM，
即NM平分∠QNR，根据角平分线定理，
$\frac{MQ}{MR}$=$\frac{NQ}{NR}$=$\frac{{S}_{△PSQ}}{{S}_{△PSR}}$，
故可填（答案不唯一）：$\frac{{S}_{△PSQ}}{{S}_{△PSR}}$．

点评 本题主要考查了合情推理中的类比推理，涉及二面角平面的定义和运算，猜测与验证，属于中档题．