
【题目】在![]() 中,点
中,点![]() ,角
,角![]() 的内角平分线所在直线的方程为
的内角平分线所在直线的方程为![]() 边上的高所在直线的方程为
边上的高所在直线的方程为![]() .
.
(Ⅰ) 求点![]() 的坐标;
的坐标;
(Ⅱ) 求![]() 的面积.
的面积.
【答案】(Ⅰ)![]() ;(Ⅱ)48.
;(Ⅱ)48.
【解析】
试题(Ⅰ)根据题意可知直线![]() 的斜率为
的斜率为![]() ,过点
,过点![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,点
,点![]() 刚好是
刚好是![]() 边上的高所在直线
边上的高所在直线![]() 与角
与角![]() 的内角平分线所在直线
的内角平分线所在直线![]() 的交点,即
的交点,即![]() , 又因为
, 又因为![]() 的内角平分线所在直线的方程为
的内角平分线所在直线的方程为![]() ,所以点
,所以点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在直线
在直线![]() 上,即可求出直线
上,即可求出直线![]() 的方程
的方程![]() ,在根据点
,在根据点![]() 是直线
是直线![]() 和
和![]() 的交点,即
的交点,即![]() 的坐标为
的坐标为![]() ;(Ⅱ)根据
;(Ⅱ)根据![]() 、
、![]() 点坐标,求出
点坐标,求出![]() ,再根据点到直线的距离公式,求出点
,再根据点到直线的距离公式,求出点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,所以
,所以![]() 的面积
的面积![]() .
.
试题解析:(Ⅰ)由题意知![]() 的斜率为-2,又点
的斜率为-2,又点![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
解方程组![]() 得
得![]()
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
又![]() 的内角平分线所在直线的方程为
的内角平分线所在直线的方程为![]() ,
,
![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在直线
在直线![]() 上,
上,
![]() 直线
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
解方程组![]() 得
得![]()
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
(Ⅱ)![]() ,
,
又直线![]() 的方程是
的方程是![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离是
的距离是 ,
,
![]() 的面积是
的面积是![]() .
.


科目:高中数学 来源: 题型:
【题目】2018年,教育部发文确定新高考改革正式启动,湖南、广东、湖北等8省市开始实行新高考制度,从2018年下学期的高一年级学生开始实行.为了适应新高考改革,某校组织了一次新高考质量测评,在成绩统计分析中,高二某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
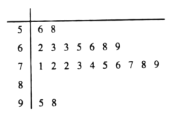
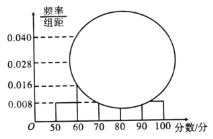
(1)求该班数学成绩在![]() 的频率及全班人数;
的频率及全班人数;
(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定![]() 分及其以上为优秀,现从该班分数在
分及其以上为优秀,现从该班分数在![]() 分及其以上的试卷中任取
分及其以上的试卷中任取![]() 份分析学生得分情况,求在抽取的
份分析学生得分情况,求在抽取的![]() 份试卷中至少有
份试卷中至少有![]() 份优秀的概率.
份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年某地遭遇严重干旱,某乡计划向上级申请支援,为上报需水量,乡长事先抽样调查100户村民的月均用水量,得到这100户村民月均用水量(单位:t)的频率分布表如下:
月均用水量分组 | 频数 | 频率 |
| 12 | |
| ||
| 40 | |
| 0.18 | |
| 6 | |
合计 | 100 | 1.00 |
(1)请完成该频率分布表,并画出相对应的频率分布直方图.
(2)样本的中位数是多少?
(3)已知上级将按每户月均用水量向该乡调水,若该乡共有1200户,请估计上级支援该乡的月调水量是多少吨.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当前,以“立德树人”为目标的课程改革正在有序推进.高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施.程度2019年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分.某学校在初三上期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到下边频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
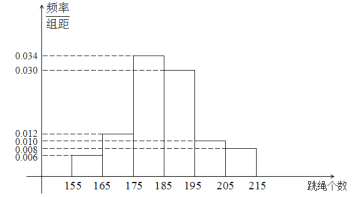
(Ⅰ)现从样本的100名学生中,任意选取2人,求两人得分之和不大于35分的概率;;
(Ⅱ)若该校初三年级所有学生的跳绳个数![]() 服从正态分布
服从正态分布![]() ,用样本数据的平均值和方差估计总体的期望和方差,已知样本方差
,用样本数据的平均值和方差估计总体的期望和方差,已知样本方差![]() (各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
(各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
![]() 预计全年级恰有2000名学生,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
预计全年级恰有2000名学生,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
![]() 若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为ξ,求随机变量的分布列和期望.
若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为ξ,求随机变量的分布列和期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交椭圆C于不同于N的A,B两点,直线NA,NB的斜率分别为k1,k2,问k1+k2是否为定值?若是的求出这个值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: ![]() ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,若点
的焦点,若点![]() 在抛物线
在抛物线![]() 上,且
上,且![]()
![]() 求抛物线
求抛物线![]() 的方程;
的方程;
![]() 动直线
动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() 其中
其中![]() ,使得向量
,使得向量![]() 与向量
与向量![]() 共线
共线![]() 其中
其中![]() 为坐标原点
为坐标原点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=![]() ,AD=2,E,F为线段AB的三等分点,G、H为线段DC的三等分点.将长方形ABCD卷成以AD为母线的圆柱W的半个侧面,AB、CD分别为圆柱W上、下底面的直径.
,AD=2,E,F为线段AB的三等分点,G、H为线段DC的三等分点.将长方形ABCD卷成以AD为母线的圆柱W的半个侧面,AB、CD分别为圆柱W上、下底面的直径.

(Ⅰ)证明:平面ADHF⊥平面BCHF;
(Ⅱ)若P为DC的中点,求三棱锥H—AGP的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com