
分析 令2x=t,则t>0,换元可得y=t2-3t+3=(t-$\frac{3}{2}$)2+$\frac{3}{4}$,由二次函数的性质可得t的范围,进而可得x的范围.
解答 解:令2x=t,则t>0,
换元可得y=t2-3t+3=(t-$\frac{3}{2}$)2+$\frac{3}{4}$,
令t2-3t+3=7可解得t=4,或t=-1(舍去),
令t2-3t+3=43可解得t=8,或t=-5(舍去),
∵y=t2-3t+3=(t-$\frac{3}{2}$)2+$\frac{3}{4}$在(0,$\frac{3}{2}$)单调递减,
在($\frac{3}{2}$,+∞)单调递增,且当t=0时y=3,当t=$\frac{3}{2}$时y=$\frac{3}{4}$,
故可得t的范围为[4,8],即2x∈[4,8],
解得x的范围为[2,3]
点评 本题考查指数函数和二次函数的值域,换元是解决问题的关键,属基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | 2或$\frac{1}{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
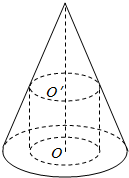 如图,圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′,下底面在圆锥SO的底面上,设圆柱OO′的体积为V1,圆锥SO的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$.
如图,圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′,下底面在圆锥SO的底面上,设圆柱OO′的体积为V1,圆锥SO的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com