

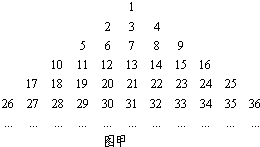
 把正整数排列成如图甲三角形数阵,然后擦去第偶行数中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,设aij位于图乙三角形数表中从上往下数第i行第j列的数,若amn=2011,则实数对(m,n)为
把正整数排列成如图甲三角形数阵,然后擦去第偶行数中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,设aij位于图乙三角形数表中从上往下数第i行第j列的数,若amn=2011,则实数对(m,n)为| k(k+1) |
| 2 |
| k(k+1) |
| 2 |
| 2011-1937 |
| 2 |


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省豫南九校高三第四次联考理科数学 题型:填空题
把正整数排列成如图甲的三角形数阵,然后擦去第偶数行中的奇数和第奇数行的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列 ,若
,若 则n=
。
则n=
。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:填空题
(理)把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列 ,若
,若 ,则
,则 __________.
__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com