
���� ������ȥ����t�����ֱ��l����ͨ���̣�����x=��cos�ȡ�y=��sin�ȣ��������C��ֱ�����귽�̣��������������M��N��ֱ�����귽�̣���ת��Ϊ�����ꣻ
������M��N��Ӧ�IJ����ֱ�Ϊt1��t2��${t_1}+{t_2}=4a+2\sqrt{3}��0$��${t_1}{t_2}=4{a^2}��0$���ɣ�
��� �⣺����$\left\{\begin{array}{l}x=-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$��tΪ��������ȥ����t�����ֱ��l����ͨ����$\sqrt{3}x+y=0$
����x=��cos�ȡ�y=��sin�ȣ��������C��ֱ�����귽��Ϊx2=y������3�֣�
��$\left\{\begin{array}{l}{x^2}=y\\ \sqrt{3}x+y=0\end{array}\right.$���$\left\{\begin{array}{l}x=0\\ y=0\end{array}\right.$��$\left\{\begin{array}{l}x=-\sqrt{3}\\ y=3\end{array}\right.$
��M��N����ļ�����ֱ�Ϊ$��2\sqrt{3}��\;\frac{2��}{3}��$����0��0������6�֣�
����P��a��0����Ȼ��ֱ��l�ϣ�
��$\left\{\begin{array}{l}x=a-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$��a��0��t����������x2=y������${t^2}-��4a+2\sqrt{3}��t+4{a^2}=0$��
��M��N��Ӧ�IJ����ֱ�Ϊt1��t2��
��a��0
��${t_1}+{t_2}=4a+2\sqrt{3}��0$��${t_1}{t_2}=4{a^2}��0$
��t1��0��t2��0
��$|PM|+|PN|={t_1}+{t_2}=4a+2\sqrt{3}=8+2\sqrt{3}$
��a=2������12�֣�
���� ���⿼���˼����귽�̡��������̡���ͨ���̵�ת������ֱ�ߵIJ��������в����ĺ��壬���ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {5��7} | B�� | {2��4} | C�� | {2��4��8} | D�� | {1��3��5��6��7} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=1 | B�� | y=$\frac{��\sqrt{x}��^{2}}{x}$ | C�� | y=$\frac{x}{x}$ | D�� | y=$\frac{|x|+1}{|x|+1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
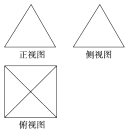 һ�������������ͼ��ͼ��ʾ������ͼ�Ͳ���ͼ���ǵȱ������Σ��Ҹü�������ĸ����ڿռ�ֱ������ϵO-xyz�е�����ֱ��ǣ�0��0��0������2��0��0������0��2��0����������������������Ϊ��������
һ�������������ͼ��ͼ��ʾ������ͼ�Ͳ���ͼ���ǵȱ������Σ��Ҹü�������ĸ����ڿռ�ֱ������ϵO-xyz�е�����ֱ��ǣ�0��0��0������2��0��0������0��2��0����������������������Ϊ��������| A�� | ��1��1��1�� | B�� | ��1��1��$\sqrt{2}$�� | C�� | ��1��1��$\sqrt{3}$�� | D�� | ��2��2��$\sqrt{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �VpΪ��?x�ʣ�1��+�ޣ���2x-1-1��0 | B�� | �VpΪ��?x�ʣ�1��+�ޣ���2x-1-1��0 | ||
| C�� | �VpΪ��?x�ʣ�-�ޣ�1]��2x-1-1��0 | D�� | �Vp�Ǽ����� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com