
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列.在欧洲,这个表叫做帕斯卡三角形,帕斯卡(1623-1662)是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,这是我国数学史上的一个伟大成就.如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列![]() ,则此数列前135项的和为( )
,则此数列前135项的和为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
利用n次二项式系数对应杨辉三角形的第n+1行,然后令x=1得到对应项的系数和,结合等比数列和等差数列的公式进行转化求解即可.
n次二项式系数对应杨辉三角形的第n+1行,
例如(x+1)2=x2+2x+1,系数分别为1,2,1,对应杨辉三角形的第3行,令x=1,就可以求出该行的系数之和,
第1行为20,第2行为21,第3行为22,以此类推
即每一行数字和为首项为1,公比为2的等比数列,
则杨辉三角形的前n项和为Sn![]() 2n﹣1,
2n﹣1,
若去除所有的为1的项,则剩下的每一行的个数为1,2,3,4,……,可以看成一个首项为1,公差为1的等差数列,
则Tn![]() ,
,
可得当n=15,在加上第16行的前15项时,所有项的个数和为135,
由于最右侧为2,3,4,5,……,为首项是2公差为1的等差数列,
则第16行的第16项为17,
则杨辉三角形的前18项的和为S18=218﹣1,
则此数列前135项的和为S18﹣35﹣17=218﹣53,
故选:A.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形。
都为矩形。

(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论。
?请证明你的结论。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分150分),每个班级20名同学,现有甲、乙两班本次考试数学分数如下列茎叶图所示:
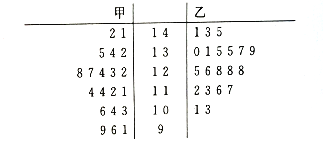
(I)根据基叶图求甲、乙两班同学数学分数的中位数,并将乙班同学的分数的频率分布直方图填充完整;
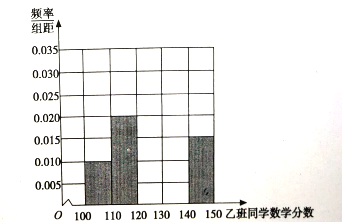
(Ⅱ)根据基叶图比较在一模考试中,甲、乙两班同学数学分数的平均水平和分数的分散程度(不要求计算出具体值,给出结论即可)
(Ⅲ)若规定分数在![]() 的成绩为良好,分数在
的成绩为良好,分数在![]() 的成绩为优秀,现从甲、乙两班成绩为优秀的同学中,按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样,共选出12位同学参加数学提优培训,求这12位同学中恰含甲、乙两班所有140分以上的同学的概率.
的成绩为优秀,现从甲、乙两班成绩为优秀的同学中,按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样,共选出12位同学参加数学提优培训,求这12位同学中恰含甲、乙两班所有140分以上的同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点坐标分别是A(7,﹣3),B(2,﹣8),C(5,1),
(1)求AB垂直平分线的方程(化为一般式);
(2)求△ABC外接圆的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)设数列{an}是公比为正数的等比数列,a1=2,a3﹣a2=12.
(1)求数列{an}的通项公式;
(2)设数列{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com