
(2)等比数列{an}中,a1+an=66,a2an-1=128,前n项的和Sn=126,求n和公比q;
(3)等比数列中q=2,S99=77,求a3+a6+…+a99;
(4)项数为奇数的等差数列{an}中,奇数项之和为80,偶数项之和为75,求此数列的中间项与项数.
思路解析:利用等差或等比数列的性质求解,要多进行整体考虑.
解:(1)由已知,得(a1+a15)-(a4+a12)-a8=2,
∴-a8=2,a8=-2,则a3+a13=2a8=-4,
S15=![]() =15a8=-30.
=15a8=-30.
(2)a1an=a2an-1=128,又a1+an=66,
∴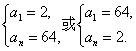
又Sn=![]() =126,
=126,
∴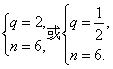
(3)∵S99=(a1+a4+…+a97)+(a2+a5+…+a98)+(a3+a6+…+a99)=(![]() +
+![]() +1)·(a3+a6+…+a99),
+1)·(a3+a6+…+a99),
∴a3+a6+…a99=![]() ×77=44.
×77=44.
(4)设等差数列{an}共有2n-1项,
则![]() =
=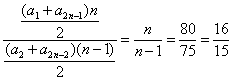
![]() n=16.
n=16.
∴此数列共31项.
中间项为a16,又S奇-S偶=(a1+a3+…+a31)-(a2+a4+…+a30)=a1+(a3-a2)(a5-a4)+…+(a31-a30)=a1+15d=a16=80-75=5.
∴a16=5.
评注:整体思想就是从整体着眼考查所研究的问题中的数列特征、结构特征,以探求解题思想,从而优化简化解题过程的思想方法.在数列中,倘若抓住等差、等比数列的项的性质,整体代值可简化解答过程.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| an3 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省南昌市莲塘一中高三(上)12月月考数学试卷(解析版) 题型:解答题
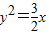 上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.
上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.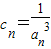 ,求证:
,求证: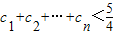 .
.查看答案和解析>>
科目:高中数学 来源:2010年高考数学新题型解析选编(6)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com