
【题目】(本小题满分14分)已知函数f(x)=-2lnx+x2-2ax+a2,其中a>0.
(Ⅰ)设g(x)为f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
【答案】(Ⅰ)当x∈(0,1)时,g'(x)<0,g(x)单调递减
当x∈(1,+∞)时,g'(x)>0,g(x)单调递增
(Ⅱ)见解析
【解析】(Ⅰ)由已知,函数f(x)的定义域为(0,+∞)
g(x)=f '(x)=2(x-1-lnx-a)
所以g'(x)=2-![]()
当x∈(0,1)时,g'(x)<0,g(x)单调递减
当x∈(1,+∞)时,g'(x)>0,g(x)单调递增
(Ⅱ)由f '(x)=2(x-1-lnx-a)=0,解得a=x-1-lnx
令Φ(x)=-2xlnx+x2-2x(x-1-lnx)+(x-1-lnx)2=(1+lnx)2-2xlnx
则Φ(1)=1>0,Φ(e)=2(2-e)<0
于是存在x0∈(1,e),使得Φ(x0)=0
令a0=x0-1-lnx0=u(x0),其中u(x)=x-1-lnx(x≥1)
由u'(x)=1-![]() ≥0知,函数u(x)在区间(1,+∞)上单调递增
≥0知,函数u(x)在区间(1,+∞)上单调递增
故0=u(1)<a0=u(x0)<u(e)=e-2<1
即a0∈(0,1)
当a=a0时,有f '(x0)=0,f(x0)=Φ(x0)=0
再由(Ⅰ)知,f '(x)在区间(1,+∞)上单调递增
当x∈(1,x0)时,f '(x)<0,从而f(x)>f(x0)=0
当x∈(x0,+∞)时,f '(x)>0,从而f(x)>f(x0)=0
又当x∈(0,1]时,f(x)=(x-a0)2-2xlnx>0
故x∈(0,+∞)时,f(x)≥0
综上所述,存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上每一点的横坐标变为原来的
上每一点的横坐标变为原来的![]() 倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,射线
轴的正半轴为极轴建立极坐标系,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,将射线
,将射线![]() 绕极点逆时针方向旋转
绕极点逆时针方向旋转![]() 交曲线
交曲线![]() 于点
于点![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数![]() 的不足近似值和过剩近似值分别为
的不足近似值和过剩近似值分别为![]() 和
和![]() ,则
,则![]() 是
是![]() 的更为精确的不足近似值或过剩近似值.我们知道
的更为精确的不足近似值或过剩近似值.我们知道![]() ,若令
,若令![]() ,则第一次用“调日法”后得
,则第一次用“调日法”后得![]() 是
是![]() 的更为精确的过剩近似值,即
的更为精确的过剩近似值,即![]() ,若每次都取最简分数,那么第四次用“调日法”后可得
,若每次都取最简分数,那么第四次用“调日法”后可得![]() 的近似分数为( )
的近似分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]()
![]() 有极值,且函数
有极值,且函数![]() 的极值点是
的极值点是![]() 的极值点,其中
的极值点,其中![]() 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若函数
时,若函数![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级体育课进行一次篮球定点投篮测试,规定每人最多投3次,每次投篮的结果相互独立.在![]() 处每投进一球得3分,在
处每投进一球得3分,在![]() 处每投进一球得2分,否则得0分.将学生得分逐次累加并用
处每投进一球得2分,否则得0分.将学生得分逐次累加并用![]() 表示,如果
表示,如果![]() 的值不低于3分就判定为通过测试,立即停止投篮,否则应继续投篮,直到投完三次为止.现有两种投篮方案:方案1:先在
的值不低于3分就判定为通过测试,立即停止投篮,否则应继续投篮,直到投完三次为止.现有两种投篮方案:方案1:先在![]() 处投一球,以后都在
处投一球,以后都在![]() 处投;方案2:都在
处投;方案2:都在![]() 处投篮.已知甲同学在
处投篮.已知甲同学在![]() 处投篮的命中率为
处投篮的命中率为![]() ,在
,在![]() 处投篮的命中率为
处投篮的命中率为![]() .
.
(1)若甲同学选择方案1,求他测试结束后所得总分![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
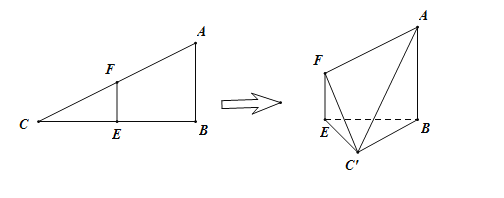
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记![]() 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,![]() 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com