
【题目】已知函数y=f(x)是定义在R上的奇函数,当x<0时,f(x)=x+1,那么不等式2f(x)﹣1<0的解集是_________
【答案】![]()
【解析】
根据题意,由奇函数的性质分析可得函数的解析式,则f(x)=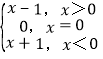 ,分3种情况讨论,求出不等式的解集,综合即可得答案.
,分3种情况讨论,求出不等式的解集,综合即可得答案.
根据题意,函数y=f(x)是定义在R上的奇函数,则f(0)=0,
设x>0,则﹣x<0,则f(﹣x)=﹣x+1,
又由函数f(x)为奇函数,则f(x)=﹣f(﹣x)=x﹣1,
则f(x)=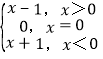 ,
,
当x>0时,2f(x)﹣1<0即2(x﹣1)﹣1<0,
变形可得:2x﹣3<0,
解可得0<x<![]() ;
;
当x=0时,2f(x)﹣1<0即﹣1<0,符合题意;
当x<0时,2f(x)﹣1<0即2(x+1)﹣1<0,
变形可得:2x+1<0,
解可得x<﹣![]() ,
,
综合可得:x的取值范围为![]() ;
;
故答案为:![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】根据我国颁布的《环境空气质量指数(![]() )技术规定》 :空气质量指数划分为
)技术规定》 :空气质量指数划分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和大于300共六个等级,对应的空气质量指数的六个等级,指数越大,等级越高 ,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数不大于150时,可以进行户外活动;当空气质量指数为151及以上时,不适合进行旅游等户外活动,下表是某市2017年11月中旬的空气质量指数情况:
和大于300共六个等级,对应的空气质量指数的六个等级,指数越大,等级越高 ,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数不大于150时,可以进行户外活动;当空气质量指数为151及以上时,不适合进行旅游等户外活动,下表是某市2017年11月中旬的空气质量指数情况:
时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| 142 | 141 | 125 | 249 | 129 | 87 | 68 | 106 | 238 | 270 |
(1)该市某市民在上述10天中随机选取1天进行户外活动,求该市民选取的这一天恰好不适合进行户外活动的概率;
(2)一名外地游客计划在上述10天中到市连续旅游2天求这10天中适合他旅游的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点![]() ,一个焦点为
,一个焦点为![]() 的椭圆被直线
的椭圆被直线![]() 截得的弦的中点的横坐标为
截得的弦的中点的横坐标为![]() .
.
(1)求此椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() 两点,且以
两点,且以![]() 为对角线的菱形的一个顶点为
为对角线的菱形的一个顶点为![]() ,求
,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点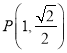 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
(![]() )求椭圆的方程.
)求椭圆的方程.
(![]() )过定点
)过定点![]() 的动直线
的动直线![]() ,交椭圆
,交椭圆![]() 于
于![]() 、
、![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .若存在,求出点
.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com