
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 为菱形且
为菱形且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)证明:直线![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(I)见解析;(II)![]() .
.
【解析】试题分析:(I)取![]() 中点
中点![]() ,可证
,可证![]() ,
, ![]() ,
, ![]() 两两互相垂直,建立以
两两互相垂直,建立以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系,得出各点坐标,可求
轴,建立空间直角坐标系,得出各点坐标,可求![]() 与平面
与平面![]() 的法向量,利用两向量垂直可证结论;(II)先求出二面角两半平面的法向量,利用法向量夹角与二面角平面角间关系可得结果.
的法向量,利用两向量垂直可证结论;(II)先求出二面角两半平面的法向量,利用法向量夹角与二面角平面角间关系可得结果.
试题解析:解法一:∵![]() ,且
,且![]() 为中点,
为中点, ![]() ,∴
,∴![]() ,
,
又 ![]() ,
, ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
又 ![]() ,∴
,∴![]() 平面
平面![]() ,
,
取![]() 中点
中点![]() ,则
,则![]() ,即
,即![]() ,
, ![]() ,
, ![]() 两两互相垂直,
两两互相垂直,
以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系如图(4), ∴
轴,建立空间直角坐标系如图(4), ∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 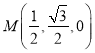

(I)  ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,取
,取![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() , ∴直线
, ∴直线![]() ∥平面
∥平面![]() .
.
(II) 设平面![]() 的法向量为
的法向量为![]() ,
, ![]() ,
,
则 ,取
,取![]() ,
,
又由(Ⅰ)知平面![]() 的法向量为
的法向量为![]() ,设二面角
,设二面角![]() 为
为![]() ,
,
∴ ,
,
∵ 二面角![]() 为锐角,∴ 二面角
为锐角,∴ 二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:取![]() 中点
中点![]() ,则
,则![]() ,即
,即![]() ,以
,以![]() 为原点,
为原点, ![]() ,
, ![]() 分别为
分别为![]() 轴,
轴,
建立空间直角坐标系如图(5),设点![]() ,
,

又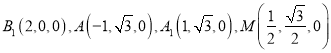 ,
, ![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴ ![]() ,
,
由 ![]() ,
, ![]() ,
, ![]() 可得:
可得:
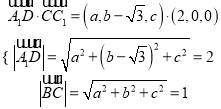 ,解得
,解得![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
下同解法二.
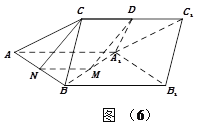
解法三:(Ⅰ)如图(6),取![]() 中点
中点![]() ,连接
,连接![]() ,则有
,则有![]() ,
,
∴![]() 为平行四边形, ∴
为平行四边形, ∴![]() ∥
∥![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴ 直线
,∴ 直线![]() ∥平面
∥平面![]() .
.
(Ⅱ)由各棱长,易得![]() ,∴
,∴![]() 平面
平面![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
如图(8),可证: ![]() 平面
平面![]() ,
,

证明![]() 平面
平面![]() ,可得
,可得![]() ,
,
故![]() 为所求的二面角的平面角,
为所求的二面角的平面角,
在![]() 中,求得:
中,求得: ![]() ,故所求的二面角的余弦值为
,故所求的二面角的余弦值为![]() .
.
解法四:
(Ⅰ)如图(7),取![]() 中点
中点![]() ,由
,由![]() ∥
∥![]() ,
,

![]() 平面
平面![]() ,∴ 直线
,∴ 直线![]() ∥平面
∥平面![]() ,
,
由![]() ∥
∥![]() ,
, ![]() 平面
平面![]() ,
,
∴ 直线![]() ∥平面
∥平面![]() ,
,
又![]() ,∴平面
,∴平面![]() ∥平面
∥平面![]() ,
,
又![]() 平面
平面![]() , ∴ 直线
, ∴ 直线![]() ∥平面
∥平面![]() .
.
(Ⅱ)同解法一.


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是BC的中点. 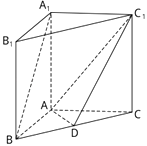
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD﹣A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为![]() .经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
.经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有![]() 个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若![]() ,求
,求![]() 个A级水样本混合化验结果不达标的概率;
个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若![]() ,现有
,现有![]() 个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,当点M(x,y)在y=f(x)的图象上运动时,点N(x﹣2,ny)在函数y=gn(x)的图象上运动(n∈N*).
,当点M(x,y)在y=f(x)的图象上运动时,点N(x﹣2,ny)在函数y=gn(x)的图象上运动(n∈N*).
(1)求y=gn(x)的表达式;
(2)若方程g1(x)=g2(x﹣2+a)有实根,求实数a的取值范围;
(3)设 ![]() ,函数F(x)=H1(x)+g1(x)(0<a≤x≤b)的值域为
,函数F(x)=H1(x)+g1(x)(0<a≤x≤b)的值域为 ![]() ,求实数a,b的值.
,求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5);求:
(1)求以向量 ![]() 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;
(2)若向量a分别与向量 ![]() 垂直,且|a|=
垂直,且|a|= ![]() ,求向量a的坐标.
,求向量a的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 能否为等差数列?若能,求其通项公式;若不能,试说明理由;
能否为等差数列?若能,求其通项公式;若不能,试说明理由;
(3)若数列![]() 是各项均为正整数的递增数列,设
是各项均为正整数的递增数列,设![]() ,则当
,则当![]() ,
, ![]() ,
, ![]() 和
和![]() ,
, ![]() ,
, ![]() 均成等差数列时,求正整数
均成等差数列时,求正整数![]() ,
, ![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com