
【题目】在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=﹣ ![]() ,AD=DC=2.
,AD=DC=2. 
(Ⅰ)求cos∠DAC及AC的长;
(Ⅱ)求BC的长.
【答案】解:(Ⅰ)△ACD中,由余弦定理可得:AC2= ![]() =
= ![]() ,解得AC=
,解得AC= ![]() . ∴cos∠DAC=
. ∴cos∠DAC= ![]() =
=  =
= ![]() .
.
(Ⅱ)设∠DAC=α=∠DCA.
由(Ⅰ)可得:cosα= ![]() ,sinα=
,sinα= ![]() .
.
∴sin∠BAC=sin(120°﹣α)= ![]() ×
× ![]() +
+ ![]() =
= ![]() .
.
∴sinB=sin(∠BAC+∠BCA)=sin(180°﹣2α)=sin2α=2× ![]() ×
× ![]() =
= ![]() .
.
在△BAC中,由正弦定理可得: ![]() =
= ![]() .
.
∴BC=  =3
=3
【解析】(1)△ACD中,由余弦定理可得:AC2= ![]() =
= ![]() ,解得AC.可得cos∠DAC=
,解得AC.可得cos∠DAC= ![]() .(2)设∠DAC=α=∠DCA.由(1)可得:cosα=
.(2)设∠DAC=α=∠DCA.由(1)可得:cosα= ![]() ,sinα=
,sinα= ![]() .可得sin∠BAC=sin(120°﹣α).sinB=sin(∠BAC+∠BCA)=sin(180°﹣2α)=sin2α.在△BAC中,由正弦定理可得:
.可得sin∠BAC=sin(120°﹣α).sinB=sin(∠BAC+∠BCA)=sin(180°﹣2α)=sin2α.在△BAC中,由正弦定理可得: ![]() =
= ![]() .即可得出.
.即可得出.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,某大型水上乐园内有一块矩形场地![]() 米,
米, ![]() 米,以
米,以![]() 为直径的半圆
为直径的半圆![]() 和半圆
和半圆![]() (半圆在矩形
(半圆在矩形![]() 内部)为两个半圆形水上主题乐园,
内部)为两个半圆形水上主题乐园, ![]() 都建有围墙,游客只能从线段
都建有围墙,游客只能从线段![]() 处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着
处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着![]() 修建不锈钢护栏,沿着线段
修建不锈钢护栏,沿着线段![]() 修建该主题乐园大门并设置检票口,其中
修建该主题乐园大门并设置检票口,其中![]() 分别为
分别为![]() 上的动点,
上的动点, ![]() ,且线段
,且线段![]() 与线段
与线段![]() 在圆心
在圆心![]() 和
和![]() 连线的同侧.已知弧线部分的修建费用为
连线的同侧.已知弧线部分的修建费用为![]() 元/米,直线部门的平均修建费用为
元/米,直线部门的平均修建费用为![]() 元/米.
元/米.
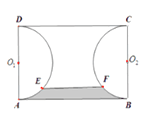
(1)若![]() 米,则检票等候区域(其中阴影部分)面积为多少平方米?
米,则检票等候区域(其中阴影部分)面积为多少平方米?
(2)试确定点![]() 的位置,使得修建费用最低.
的位置,使得修建费用最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参与舒城中学数学选修课的同学对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图.
定价x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

参考数据:
![]() ,
,
![]() .
.
(1)根据散点图判断y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)当定价为150元/千克时,试估计年销量.
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣4|,g(x)=|2x+1|.
(1)解不等式f(x)<g(x);
(2)若2f(x)+g(x)>ax对任意的实数x恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ea(x﹣1)﹣ax2 , a为不等于零的常数.
(Ⅰ)当a<0时,求函数f′(x)的零点个数;
(Ⅱ)若对任意x1 , x2 , 当x1<x2时,f(x2)﹣f(x1)>a( ![]() ﹣2x1)(x2﹣x1)恒成立,求实数a的取值范围.
﹣2x1)(x2﹣x1)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的两焦点为![]() ,
,![]() ,离心率
,离心率![]() .
.
(1)求此椭圆的方程;
(2)设直线![]() :
:![]() ,若
,若![]() 与此椭圆相交于
与此椭圆相交于![]() ,
,![]() 两点,且
两点,且![]() 等于椭圆的短轴长,求
等于椭圆的短轴长,求![]() 的值;
的值;
(3)以此椭圆的上顶点![]() 为直角顶点作椭圆的内接等腰直角三角形
为直角顶点作椭圆的内接等腰直角三角形![]() ,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由.
,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商计划销售一款新型的空气净化器,经市场调研发现以下规律:当每台净化器的利润为 x (单位:元, x 0 )时,销售量 q(x) (单位:百台)与 x 的关系满足:若 x 不超过 20 , 则 ![]() ;若 x 大于或等于180 ,则销售量为零;当 20 ≤ x ≤180 时,
;若 x 大于或等于180 ,则销售量为零;当 20 ≤ x ≤180 时,![]() ( a , b 为实常数).
( a , b 为实常数).
(Ⅰ)求函数 q(x) 的表达式;
(Ⅱ)当 x 为多少时,总利润(单位:元)取得最大值,并求出该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)![]() 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求![]() 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数).
为这三个数的中位数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com