
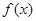 ,若在定义域存在实数
,若在定义域存在实数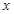 ,满足
,满足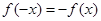 ,则称
,则称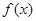 为“局部奇函数”.
为“局部奇函数”.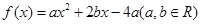 ,试判断
,试判断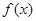 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;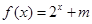 是定义在
是定义在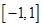 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数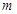 的取值范围.
的取值范围.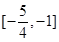 .
.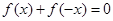 ,如果这个方程有实数解,就说明
,如果这个方程有实数解,就说明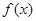 是“局部奇函数”,如果这个方程无实数解,就说明
是“局部奇函数”,如果这个方程无实数解,就说明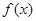 不是“局部奇函数”,易知
不是“局部奇函数”,易知 有实数解,因此答案是肯定的;(2)已经明确
有实数解,因此答案是肯定的;(2)已经明确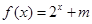 是“局部奇函数”,也就是说方程
是“局部奇函数”,也就是说方程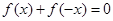 一定有实数解,问题也就变成方程
一定有实数解,问题也就变成方程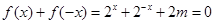 在
在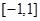 上有解,求参数
上有解,求参数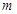 的取值范围,又方程可变形为
的取值范围,又方程可变形为 ,因此求
,因此求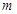 的取值范围,就相当于求函数
的取值范围,就相当于求函数
 的值域,用换元法(设
的值域,用换元法(设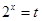 ),再借助于函数
),再借助于函数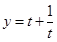 的单调性就可求出.
的单调性就可求出.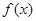 为“局部奇函数”等价于关于
为“局部奇函数”等价于关于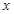 的方程
的方程 有解.
有解.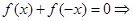
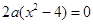 (3分)
(3分)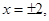
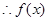 为“局部奇函数”.(5分)
为“局部奇函数”.(5分)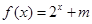 时,
时, 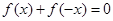 可转化为
可转化为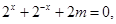 (8分)
(8分)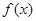 的定义域为
的定义域为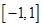 ,所以方程
,所以方程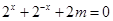 在
在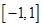 上有解,令
上有解,令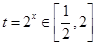 ,(9分)
,(9分)
 在
在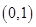 上递减,在
上递减,在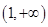 上递增,
上递增,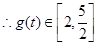 (11分)
(11分) (12分)
(12分)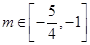 (14分)
(14分)

科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 |
| C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
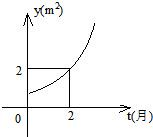
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①② | B.②③ | C.②④ | D.①③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
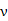 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度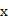 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当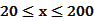 时,车流速度
时,车流速度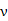 是车流密度
是车流密度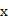 的一次函数。
的一次函数。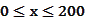 时,求函数
时,求函数 的表达式;
的表达式;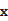 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)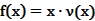 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com