
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求a的值,并证明![]() 是R上的增函数;
是R上的增函数;
(2)若关于t的不等式f(t2-2t)+f(2t2-k)<0的解集非空,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2+alnx.
x2+alnx.
(1)若a=﹣1,求函数f(x)的极值,并指出极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在g(x)=![]() x3的图象下方.
x3的图象下方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是
A. 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小
B. 在回归直线方程![]() =0.2x+0.8中,当解释变量x每增加1个单位时,预报变量
=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
C. 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
D. 回归直线过样本点的中心(![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某影院共有1000个座位,票价不分等次,根据该影院的经营经验,当每张票价不超过10元时,票可全部售出,当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院一个合适的票价,符合的基本条件是:
①为了方便找零和算账,票价定为1元的整数倍;
②影院放映一场电影的成本费为5750元,票房收入必须高于成本支出.
(1)设定价为![]() (
(![]() )元,净收入为
)元,净收入为![]() 元,求
元,求![]() 关于
关于![]() 的表达式;
的表达式;
(2)每张票价定为多少元时,放映一场的净收入最多?此时放映一场的净收入为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (限定
(限定![]() ).
).
(1)写出曲线![]() 的极坐标方程,并求
的极坐标方程,并求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(2)射线![]() 与曲线
与曲线![]() 与
与![]() 分别交于点
分别交于点![]() (
(![]() 异于原点),求
异于原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25![]() (分贝),并规定测试值在区间
(分贝),并规定测试值在区间![]() 为非常优秀,测试值在区间
为非常优秀,测试值在区间![]() 为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:

(Ⅰ)现从听力等级为![]() 的同学中任意抽取出4人,记听力非常优秀的同学人数为
的同学中任意抽取出4人,记听力非常优秀的同学人数为![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(Ⅱ)在(Ⅰ)中抽出的4人中任选一人参加一个更高级别的听力测试,测试规则如下:四个音叉的发生情况不同,由强到弱的次序分别为1,2,3,4.测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号![]() ,
, ![]() ,
, ![]() ,
, ![]() (其中
(其中![]() ,
, ![]() ,
, ![]() ,
, ![]() 为1,2,3,4的一个排列).若
为1,2,3,4的一个排列).若![]() 为两次排序偏离程度的一种描述,
为两次排序偏离程度的一种描述, ![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
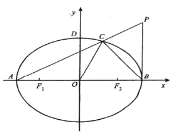
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为左,右焦点,
分别为左,右焦点,![]() 分别为左,右顶点,D为上顶点,原点
分别为左,右顶点,D为上顶点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设点
.设点![]() 在第一象限,纵坐标为t,且
在第一象限,纵坐标为t,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)(文)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求直线
的面积,求直线![]() 的方程;
的方程;
(理)求过点![]() 的圆方程(结果用t表示)
的圆方程(结果用t表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com