四面体的六条棱中,有五条棱长都等于a.
(Ⅰ)求该四面体的体积的最大值;
(Ⅱ)当四面体的体积最大时,求其表面积.
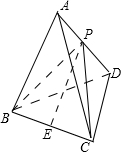
解:(Ⅰ)如图,
在四面体ABCD中,设AB=BC=CD=AC=BD=a,AD=x,取AD的中点为P,
BC的中点为E,连接BP、EP、CP.
∵AB=BD,P为AD中点,∴BP⊥AD,
∵AC=CD,P为AD中点,∴PC⊥AD,
又BP∩PC=P,∴AD⊥平面BPC,
∴V
A-BCD=V
A-BPC+V
D-BPC=

S
△BPC•AP+

S
△BPC•PD
=

S
△BPC•AD
=

×

a×
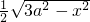
•x
=

≤
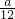
•
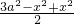
=

a
3(当且仅当x=

a时取“=”).
∴该四面体的体积的最大值为

a
3.
(Ⅱ)由(1)知,△ABC和△BCD都是边长为a的正三角形,
△ABD和△ACD是全等的等腰三角形,其腰长为a,底边长为

a,
∴S
△ABC=S
△BCD=
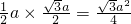
,
S
△ABD=S
△ACD=
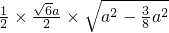
=
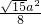
所以当四面体的体积最大时,其表面积S=
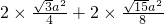
=
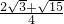
a
2.
分析:(Ⅰ)设出四面体A-BCD,不妨设棱AB、AC、BC、BD、CD相等且为定值a,把棱AD看作动的棱,设为x,取AD的中点P,
连接BP、CP后,四面体A-BCD分成了两个同底面的三棱锥A-BPC和D-BPC,四面体的体积转化为此两个三棱锥的体积和,整理后化为关于x的函数,然后运用基本不等式求四面体体积的最大值.
(Ⅱ)求出使四面体体积最大时的x的值,四面体的表面积就是表面四个三角形的面积和,可直接运用三角形的面积求解.
点评:本题考查了棱锥的体积和表面积,考查了学生的空间想象能力和数学转化能力,考查了函数思想,运用了基本不等式求函数的最值,此题是中档题.

 解:(Ⅰ)如图,
解:(Ⅰ)如图, S△BPC•AP+
S△BPC•AP+ S△BPC•PD
S△BPC•PD S△BPC•AD
S△BPC•AD ×
× a×
a×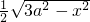 •x
•x ≤
≤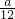 •
•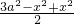 =
= a3(当且仅当x=
a3(当且仅当x= a时取“=”).
a时取“=”). a3.
a3. a,
a,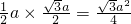 ,
,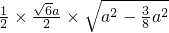 =
=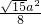
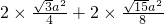 =
=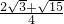 a2.
a2.
