
给出下列命题:①对空间任意两个向量![]() (
(![]() ≠
≠![]() ),则
),则![]() ∥
∥![]() 的充要条件是存在实数
的充要条件是存在实数![]() ,使得
,使得![]() ; ②若
; ②若![]() ,则
,则![]() ; ③若
; ③若![]() 不能构成空间的一个基底,则O,A,B,C四点共面; ④对于非零向量
不能构成空间的一个基底,则O,A,B,C四点共面; ④对于非零向量![]() ,则
,则![]() 一定成立. 正确命题的个数为( )
一定成立. 正确命题的个数为( )
A.1 B.2 C. 3 D. 4
科目:高中数学 来源: 题型:
| x2 |
| 5 |
| y2 |
| m |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 恒有公共点,实数m的取值范围是m≥1
恒有公共点,实数m的取值范围是m≥1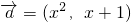 ,
,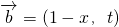 ,若函数f(x)=
,若函数f(x)= 在区间上是增函数,则实数t的取值范围是(5,+∞);
在区间上是增函数,则实数t的取值范围是(5,+∞);查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都九中高三(下)3月月考数学试卷(文科)(解析版) 题型:解答题
 恒有公共点,实数m的取值范围是m≥1
恒有公共点,实数m的取值范围是m≥1 ,
, ,若函数f(x)=
,若函数f(x)= 在区间上是增函数,则实数t的取值范围是(5,+∞);
在区间上是增函数,则实数t的取值范围是(5,+∞);查看答案和解析>>
科目:高中数学 来源: 题型:
设G是一个非空集合, 若对G 中任意两个元素a,b通过某个法则“![]() ”, G中有唯一确定的元素c与之对应, 则称法则“
”, G中有唯一确定的元素c与之对应, 则称法则“![]() ”为G集合上的一个代数运算. 如果G的这个代数运算还满足:(1)对任意a、b、c
”为G集合上的一个代数运算. 如果G的这个代数运算还满足:(1)对任意a、b、c![]() G,有
G,有![]() ;(2)G中有元素e使对每个a
;(2)G中有元素e使对每个a![]() G都有
G都有![]() ;(3)对G中每个元素a,存在元素
;(3)对G中每个元素a,存在元素![]() 使
使![]() ,则称G关于代数运算“
,则称G关于代数运算“![]() ”构成一个群.给出下列命题:
”构成一个群.给出下列命题:
① 有理数的加法运算是有理数集Q上的代数运算;
② 有理数的除法运算是有理数集Q上的代数运算;
③ 全体非零实数集关于实数的乘法运算构成一个群;
④ 全体复数集关于复数的除法运算构成一个群.
其中正确命题的序号是 (填上所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
设G是一个非空集合, 若对G 中任意两个元素a,b通过某个法则“![]() ”, G中有唯一确定的元素c与之对应, 则称法则“
”, G中有唯一确定的元素c与之对应, 则称法则“![]() ”为G集合上的一个代数运算. 如果G的这个代数运算还满足:(1)对任意a、b、c
”为G集合上的一个代数运算. 如果G的这个代数运算还满足:(1)对任意a、b、c![]() G,有
G,有![]() ;(2)G中有元素e使对每个a
;(2)G中有元素e使对每个a![]() G都有
G都有![]() ;(3)对G中每个元素a,存在元素
;(3)对G中每个元素a,存在元素![]() 使
使![]() ,则称G关于代数运算“
,则称G关于代数运算“![]() ”构成一个群.给出下列命题:
”构成一个群.给出下列命题:
① 有理数的加法运算是有理数集Q上的代数运算;
② 有理数的除法运算是有理数集Q上的代数运算;
③ 全体非零实数集关于实数的乘法运算构成一个群;
④ 全体复数集关于复数的除法运算构成一个群.
其中正确命题的序号是 (填上所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com