
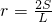 ;根据类比思想,若四面体体积和表面积分别为V、P,其内切球半径为R,则R=________.
;根据类比思想,若四面体体积和表面积分别为V、P,其内切球半径为R,则R=________. 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:2012届浙江省温州市高三八校联考理科数学 题型:解答题
.本小题满分15分)
如图,已知椭圆E: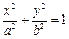
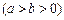 ,焦点为
,焦点为 、
、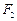 ,双曲线G:
,双曲线G: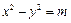
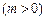 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设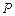 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线 、
、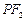 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形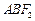 的周长等于
的周长等于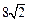 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为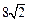 .
.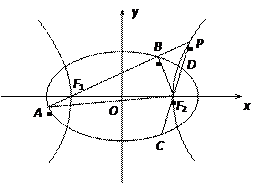
(1)求椭圆E与双曲线G的方程;
(2)设直线 、
、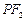 的斜率分别为
的斜率分别为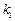 和
和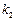 ,探求
,探求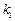 和
和
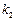 的关系;
的关系;
(3)是否存在常数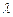 ,使得
,使得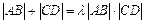 恒成立?
恒成立?
若存在,试求出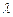 的值;若不存在, 请说明理由.
的值;若不存在, 请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省温州市高三八校联考理科数学 题型:解答题
.本小题满分15分)
如图,已知椭圆E: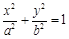
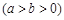 ,焦点为
,焦点为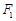 、
、 ,双曲线G:
,双曲线G: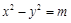
 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设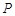 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线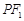 、
、 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形 的周长等于
的周长等于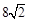 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为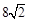 .
.
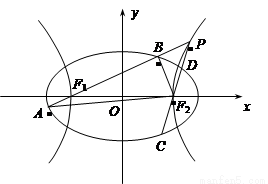
(1)求椭圆E与双曲线G的方程;
(2)设直线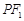 、
、 的斜率分别为
的斜率分别为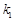 和
和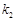 ,探求
,探求
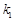 和
和
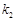 的关系;
的关系;
(3)是否存在常数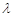 ,使得
,使得 恒成立?
恒成立?
若存在,试求出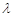 的值;若不存在,
请说明理由.
的值;若不存在,
请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三下学期开学质量检测数学试卷 题型:解答题
(本小题满分14分)如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在该空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
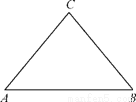
(1) 若小路一端E为AC的中点,求此时小路的长度;
(2) 求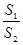 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题18分,第(1)小题4分;第(2)小题6分;第(3)小题8分)
如图,已知椭圆E:![]()
![]() ,焦点为
,焦点为![]() 、
、![]() ,双曲线G:
,双曲线G:![]()
![]() 的顶点是该椭圆的焦点,设
的顶点是该椭圆的焦点,设![]() 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线![]() 、
、![]() 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形![]() 的周长等于
的周长等于![]() ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为![]() .
.
(1)求椭圆E与双曲线G的方程;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,探求
,探求![]() 和
和![]() 的关系;
的关系;
 (3)是否存在常数
(3)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,试求出
恒成立?若存在,试求出![]() 的值;若不存在,
的值;若不存在,
请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com