
【题目】已知![]() 。
。
(1)曲线![]() 在点
在点![]() 处的切线的斜率小于
处的切线的斜率小于![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)对任意的![]() ,函数
,函数![]() 在区间
在区间![]() 上为增函数,求
上为增函数,求![]() 的取值范围。
的取值范围。
【答案】(1) f(x)的增区间为(0,1),(2a+1,+∞);减区间为(1,2a+1);
(2) [8,+∞).
【解析】(1)函数f(x)=![]() x2﹣(2a+2)x+(2a+1)lnx,(x>0),
x2﹣(2a+2)x+(2a+1)lnx,(x>0),
f′(x)=x﹣(2a+2)+![]() =
=![]() ,x>0,
,x>0,
由题意可得f′(2)=![]() <0,可得a>
<0,可得a>![]() ,2a+1>2>1,
,2a+1>2>1,
由f′(x)>0,可得x>2a+1或0<x<1;f′(x)<0,可得1<x<2a+1.
即有f(x)的增区间为(0,1),(2a+1,+∞);减区间为(1,2a+1);
(2)∵函数g(x)=f(x)﹣![]() 在区间[1,2]上为增函数,
在区间[1,2]上为增函数,
∴g′(x)≥0对任意的a∈[![]() ,
,![]() ],x∈[1,2]恒成立,
],x∈[1,2]恒成立,
即x﹣(2a+2)+![]() +
+![]() ≥0,即为x3﹣(2a+2)x2+(2a+1)x+λ≥0,
≥0,即为x3﹣(2a+2)x2+(2a+1)x+λ≥0,
则(2x﹣2x2)a+x3﹣2x2+x+λ≥0,a∈[![]() ,
,![]() ],
],
由x∈[1,2],可得2x﹣2x2≤0,只需![]() (2x﹣2x2)+x3﹣2x2+x+λ≥0.
(2x﹣2x2)+x3﹣2x2+x+λ≥0.
即x3﹣7x2+6x+λ≥0对x∈[1,2]恒成立,
令h(x)=x3﹣7x2+6x+λ,h′(x)=3x2﹣14x+6≤0在1≤x≤2恒成立,
则有h(x)在[1,2]递减,可得h(2)取得最小值,且为﹣8+λ≥0,
解得λ≥8,
∴λ的取值范围是[8,+∞).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=ex﹣ax(a∈R),e为自然对数的底数.
(1)若a=1时,求曲线y=f(x)在x=0处的切线方程;
(2)求函数f(x)在[0,1]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,
为顶点, ![]() 轴为对称轴的抛物线,且焦点在
轴为对称轴的抛物线,且焦点在![]() 轴正半轴上,圆
轴正半轴上,圆![]() .过焦点
.过焦点![]() 且与
且与![]() 轴平行的直线与抛物线交于
轴平行的直线与抛物线交于![]() 两点,且
两点,且![]() .
.
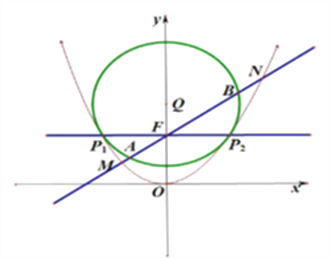
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)直线![]() 过
过![]() 且与抛物线
且与抛物线![]() 和圆
和圆![]() 依次交于
依次交于![]() ,且直线
,且直线![]() 的斜率
的斜率![]() ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ) ![]() 在某一个周期内的图象时,列表并填入了部分数据,如表:
在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
f(x)=Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将如表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位长度,得到函数y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
个单位长度,得到函数y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
(3)求当 ![]() 时,函数y=g(x)的值域.
时,函数y=g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( ) 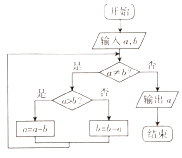
A.30
B.18
C.5
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个不透明的盒子里有5枚质地均匀、大小相等的铜币,铜币有两种颜色,一种为黄色,一种为绿色.其中黄色铜币两枚,标号分别为1,2,绿色铜币三枚,标号分别为1,2,3.
(1)从该盒子中任取2枚,试列出一次实验所有可能出现的结果;
(2)从该盒子中任取2枚,求这两枚铜币颜色不同且标号之和大于3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首项为正数的数列{an}满足an+1=(a+3),n∈N*.
(1)证明:若a1为奇数,则对一切n≥2,an都是奇数;
(2)若对一切n∈N*都有an+1>an , 求a1的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com