
分析 (1)f′(x)=lnx+1+2x-a=lnx-(-2x+a-1),当x=t时,f′(t)=0,作出图象,利用数形结合思想能求出a的范围.
(2)由 f′(t)=0,t>1,作出f(x)的大致图象,由此能证明x1+x2>2.
(3)由导数性质能构造函数,利用导数研究函数的单调性,由此能证明x1•x2>1.
解答 解:(1)∵f(x)=xlnx+x2-ax+2(a∈R),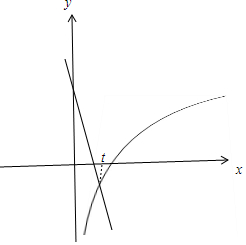
∴f′(x)=lnx+1+2x-a=lnx-(-2x+a-1),
当x=t时,f′(t)=0,如右上图,
由图知:x∈(0,t)时,f′(x)<0,f(x)是减函数,
x∈(t,+∞)时,f′(x)>0,f(x)是增函数,
∵函数f(x)=xlnx+x2-ax+2(a∈R)有两个不同的零点x1,x2.
∴f(t)<0,
∵f′(t)=lnt-(-2t+a-1)=0,即lnt=-2t+a-1,
∴f(t)=t(-2t+a-1)+t2-at+2=-t2-t+2<0,
即t2+t-2>0,
∴t>1或t<-2(舍),
当t=1时,ln1=-2+a-1,解得a=3,
∵t>1,∴a>3.
证明:(2)由(1)知 f′(t)=0,t>1,
∵函数f(x)=xlnx+x2-ax+2(a∈R)有两个不同的零点x1,x2.
f(x)的定义域为(0,+∞),
∴由x1,x2∈(0,+∞),令x1<x2.
∴f(x)的大致图象如右下图:
∴$\frac{{x}_{1}+{x}_{2}}{2}=t>1$,
∴x1+x2>2.
(3)由(2)知,x1,x2∈(0,+∞),x1+x2>2,
∵函数f(x)=xlnx+x2-ax+2(a∈R)有两个不同的零点x1,x2,a>3,
∴f(x2)=${x}_{2}ln{x}_{2}+{{x}_{2}}^{2}$-ax${{\;}_{2}}^{\;}$+2=0,∴a=lnx2+x2+$\frac{2}{{x}_{2}}$,
f($\frac{1}{{x}_{2}}$)=$\frac{1}{{x}_{2}}ln\frac{1}{{x}_{2}}$+$\frac{1}{{{x}_{2}}^{2}}$-x2lnx2-x22,
设h(k)=klnk+k2-$\frac{1}{k}ln\frac{1}{k}$-$\frac{1}{{k}^{2}}$=(k+$\frac{1}{k}$)lnk+k2-$\frac{1}{{k}^{2}}$,
h′(k)=(1-$\frac{1}{{k}^{2}}$)lnk+1+$\frac{1}{{k}^{2}}$+2k+$\frac{2}{{k}^{3}}$>0,
∴h(k)是(0,+∞)上的增函数,
∴当k>1时,h(k)>h(1)=0,
∵x2>1,∴$\frac{1}{{x}_{2}}$<1,∴h($\frac{1}{{x}_{2}}$)<h(1)=0,
又由零点性质得h(x1)=0,
∴h(x1)>h($\frac{1}{{x}_{2}}$),∴x1>$\frac{1}{{x}_{2}}$,
∴x1•x2>1.
点评 本题考查实数的取值范围的求法,考查不等式的证明,根据条件构造函数,利用导数研究函数的单调性是解决本题的关键.综合性较强,难度较大.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 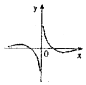 | B. | 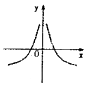 | C. | 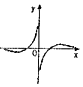 | D. | 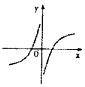 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac2>bc2 | B. | 若a>b,c>d,则a-c>b-d | ||
| C. | 若a>b,则$\frac{1}{a}<\frac{1}{b}$ | D. | 若a>|b|,则a2>b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com