
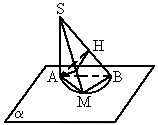
如图,平面α内有一个半圆,直径为AB,过A作SA⊥平面α,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.
(1)求证:NH⊥SB;
(2)这个图形中有多少个线面垂直关系?
(3)这个图形中有多少个直角三角形?
|
(1) 证明:连AM、BM.∵AB为已知半圆直径,∴AM⊥BM.∵SA⊥平面α,MB α,∴SA⊥MB.∵AM∩SA=A,∴MB上面SAM.∵AN α,∴SA⊥MB.∵AM∩SA=A,∴MB上面SAM.∵AN 面SAW,∴BM⊥AN.∵AN⊥SM,∴AN⊥面SMB.∵AH⊥SB于H,则NH为AH在面SMB内的射影,∴NH⊥SB 面SAW,∴BM⊥AN.∵AN⊥SM,∴AN⊥面SMB.∵AH⊥SB于H,则NH为AH在面SMB内的射影,∴NH⊥SB
(2) 解:由(1)知,SA⊥面AMB,BM⊥面SAM,AN⊥面SMB.∵SB⊥AH且SB⊥HN,∴SB⊥平面ANH.∴图中共有4个线面垂直关系.(3) 解:∵SA⊥平面AMB,∴△ SAB、△SAM均为直角三角形.∵ BM⊥平面SAM,∴△ BMA、△BMS均为直角三角形.∴ AN⊥平面SMB,∴△ ANM、△ANH、△ANS均为直角三角形.∵ SB⊥平面AHN,∴△ SHA、△BHA、△SHN均为直角三角形.综上所述,图中共有 10个直角三角形.本题是考查直线与直线的垂直、直线与平面垂直的判定,解题时以空间的眼光观察图形,正确地发现线面的位置关系.本题的创新之处在于把垂直关系的空间化,打破学生头脑中国有的平面垂直位置关系模式,锻炼了空间想象能力,深化了对三垂线定理及逆定理的理解. |


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径,AA1=AC=CB=2.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径,AA1=AC=CB=2.查看答案和解析>>
科目:高中数学 来源: 题型:
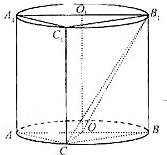 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
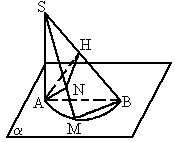
如图,平面a内有一个半圆,直径为AB,过A作SA⊥平面a,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.这个图形中有多少对垂直的直线?
查看答案和解析>>
科目:高中数学 来源: 题型:044
如图,平面
a内有一个半圆,直径为AB,过A作SA⊥平面a,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.这个图形中有多少对垂直的直线?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com