某厂拟生产甲、乙两种试销产品,每件销售收入分别为3千元、2千元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B上加工一件甲所需工时分别为1工时、2工时,加工一件乙所需工时分别为2工时、1工时,A、B两种设备每月有效使用台时数为a(400≤a≤500).求生产收入最大值的范围.
分析:先设甲、乙两种产品月产量分别为x、y件,写出约束条件、目标函数,欲求生产收入最大值的范围,即求可行域中的最优解,在线性规划的解答题中建议使用直线平移法求出最优解,即将目标函数看成是一条直线,分析目标函数Z与直线截距的关系,进而求出最优解.注意:最后要将所求最优解还原为实际问题.
解答: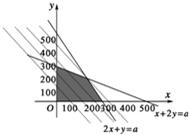
解:设甲、乙两种产品月产量分别为x、y件,
约束条件是
目标函数是z=3x+2y,
由约束条件画出可行域,如图.将z=3x+2y变形为y=-
x+
,
这是斜率为-
,随z变化的一簇直线.
是直线在y轴上的截距,当
最大时z最大,
当然直线要与可行域相交,即在满足约束条件时目标函数取得最大值.
由
解得
在这个问题中,使z=3x+2y取得最大值的(x,y)是两直线2x+y=a与x+2y=a的交点(
,
).
∴z=3•
+2•
=
a.
又∵400≤a≤500
,∴
≤z≤
.
故月生产收入最大值的范围是[
,
].
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中.

 解:设甲、乙两种产品月产量分别为x、y件,
解:设甲、乙两种产品月产量分别为x、y件,
