
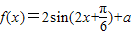 a∈R,a是常数
a∈R,a是常数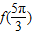 的值
的值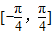 上的最大值与最小值之和为
上的最大值与最小值之和为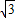 ,求实数a的值.
,求实数a的值.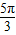 代入f(x)=2sin(2x+
代入f(x)=2sin(2x+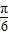 )+a,可求得f(
)+a,可求得f(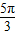 );
);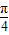 ,
,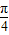 ],可求得2x+
],可求得2x+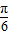 ∈[-
∈[-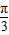 ,
, ],继而可得sin(2x+
],继而可得sin(2x+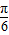 )∈[-
)∈[-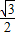 ,1],结合题意即可求得a的值.
,1],结合题意即可求得a的值. )+a,a∈R,
)+a,a∈R, )=2sin(
)=2sin(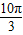 +
+ )+a=-2+a…(3分)
)+a=-2+a…(3分)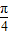 ,
, ],
], ∈[-
∈[-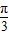 ,
,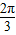 ],
],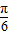 )∈[-
)∈[- ,1]…(6分)
,1]…(6分)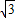 +a≤f(x)≤2+a…(9分)
+a≤f(x)≤2+a…(9分) +a,由已知得-
+a,由已知得-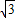 +a+a+2=
+a+a+2=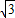
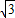 -1…(12分)
-1…(12分)

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
| 1 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2009-2010学年辽宁省沈阳市东北育才学校高三(下)5月月考数学试卷(理科)(解析版) 题型:解答题
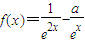 ,其中a∈R.
,其中a∈R. ,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).
,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com