练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知sinα+cosα=$\frac{\sqrt{3}}{2}$，且α∈（0，π），则sin2α的值为（　　）
    A．-$\frac{\sqrt{15}}{4}$B．-$\frac{1}{4}$C．$\frac{\sqrt{15}}{4}$D．$\frac{1}{4}$

    分析 由条件利用同角三角函数的基本关系，求得sin2α的值．

    解答 解：∵已知sinα+cosα=$\frac{\sqrt{3}}{2}$，且α∈（0，π），平方可得1+sin2α=$\frac{3}{4}$，
    ∴sin2α=-$\frac{1}{4}$，
    故选：B．

    点评 本题主要考查同角三角函数的基本关系的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．某工厂第三年的产量比第一年的产量增加20%，若每年的平均增长率相同（设为x），则以下结论正确的是（　　）
    A．x=10%B．x＜10%
    C．x＞10%D．x的大小由第一年的产量决定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知集合A={x|（x+1）（x-2）＜0}，非空集合B={x|2a＜x＜6}，则“A∩B=∅”的充分不必要条件可以是（　　）
    A．-1＜a＜2B．1≤a＜3C．a＞0D．1＜a＜3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数y=f（x）上任一点（x0，f（x0））处的切线斜率$k=（{{x_0}-2}）{（{{x_0}+1}）^2}$，则该函数的单调递减区间为（　　）
    A．[-1，+∞）B．（-∞，2]C．（-∞，-1），（1，2）D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

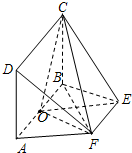    19．如图，AB为圆O的直径，点E、F在圆O上，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
    （Ⅰ）求证：AF⊥平面CBF；
    （Ⅱ）若AF=BE，求二面角的E-OC-F的余弦值大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．如图，平面四边形ABCD中，AB=$\sqrt{5}$，AD=2$\sqrt{2}$，CD=$\sqrt{3}$，∠CBD=30°，∠BCD=120°，则△ADC的面积S为$\frac{3+\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．集合A={-1，1}，B={x|mx=1}，A∪B=A，则实数m组成的集合（　　）
    A．{-1}B．{1}C．{-1，1}D．{-1，0，1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=-2sin2x+2$\sqrt{3}$sinxcosx+1．
    （1）求f（x）的最小正周期及单调减区间；
    （2）若x∈[-$\frac{π}{6}$，$\frac{π}{3}$]，求f（x）的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若E，F，G分别为正三角形ABC的边AB，BC，CA的中点，以△EFG为底面，把△AEG，△BEF，△CFG折起使A，B，C重合为一点P，则下列关于线段PE与FG的论述不正确的为（　　）
    A．垂直B．长度相等C．异面D．夹角为60°

    查看答案和解析>>

    同步练习册答案