
(1)设ak(1≤k≤n)为第k位职工所得奖金额,试求a2、a3,并用k、n和b表示ak ;(不必证明)
(2)证明a k>a k+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
(3)发展基金与n和b有关,记为Pn(b).对常数b,当n变化时,求![]() Pn(b).
Pn(b).
 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
| b |
| n |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| n |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(Ⅰ)设ak(1≤k≤n)为第k位职工所得奖金额,试求a2、a3,并用k、n和b表示ak;(不必证明)
(Ⅱ)证明ak>ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
(Ⅲ)发展基金与n和b有关,记为Pn(b).对常数b,当n变化时,求![]() Pn(b).
Pn(b).
查看答案和解析>>
科目:高中数学 来源:上海 题型:解答题
| b |
| n |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| n |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:14.6 函数的连续性及极限的应用(解析版) 题型:解答题
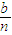 元,然后将余额除以n发给第2位职工,按此方案将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后将余额除以n发给第2位职工,按此方案将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.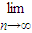 Pn(b)(可用公式
Pn(b)(可用公式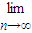 (1-
(1-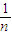 )n=
)n=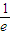 ).
).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com